Modélisation du contact : les liaisons parfaites
Définition : Liaison parfaite
Une liaison parfaite entre deux solides indéformables est telle que :
les surfaces de contact sont géométriquement parfaites (plan, cylindre, etc. parfaits ) ;
le contact s'effectue sans frottement ;
le jeu de fonctionnement est nul.
Définition : Torseur cinématique d'une liaison parfaite
Soit un solide \(S_1\) en liaison avec le solide \(S_0\). Le torseur cinématique de la liaison \(L_{1/0}\), est le torseur distributeur des vitesses du solide \(S_1\) par rapport au solide \(S_0\) liés entre eux par la liaison \(L_{1/0}\).
En théorie, sans contact entre \(S_1\) et \(S_0\), ce torseur cinématique comporte 6 composantes scalaires :
Dès que \(S_1\) et \(S_0\) sont mis en contact, certains degrés de liberté sont supprimés. En choisissant une base judicieusement orientée par rapport aux contacts, certaines composantes du torseur s'annulent.
Ils existe 11 liaisons normalisées traduisant autant de dispositions possibles des contacts entre \(S_1\) et \(S_0\). Pour chacune d'entre elles, il faut être en mesure de donner :
la désignation normalisée complète de la liaison, c'est à dire son nom (pivot, glissière, etc.) ainsi que ses caractéristiques géométriques (axe, direction, centre, etc.).
ses représentations normalisées planes et spatiale,
les composantes de son torseur cinématique,
les particularités de ce torseur, c'est à dire l'ensemble des points et la base pour lesquels l'expression ou la forme littérale du torseur est conservée.
Remarque :
La base d'expression \((\vec x, \vec y, \vec z)\) et le point de réduction \(A\) sont usuellement choisis pour que les composantes de \(\overrightarrow{\Omega(S_1/S_0)}\) et \(\overrightarrow{V_{A\in S_1/S_0}}\) soient les plus simples possible. C'est-à-dire de manière à faire apparaître le plus de zéros possible dans la notation « colonne » du torseurs.
Liaisons élémentaires
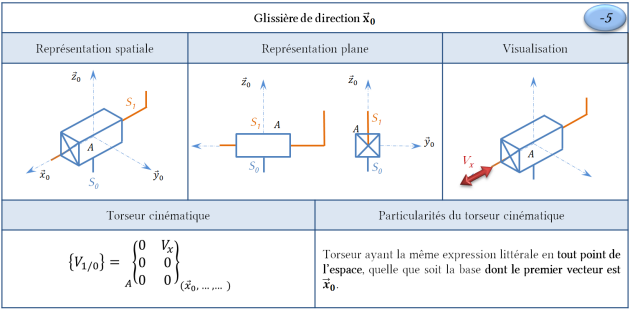
Ces 6 liaisons décrites ci-dessous sont dites élémentaires (ou simples) car elles peuvent être obtenues en associant deux surfaces élémentaires de type plan, cylindre de révolution ou sphère.
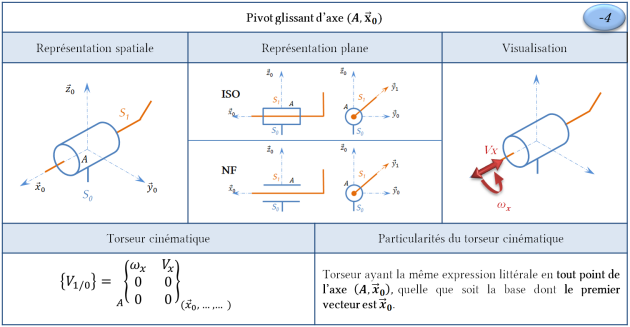
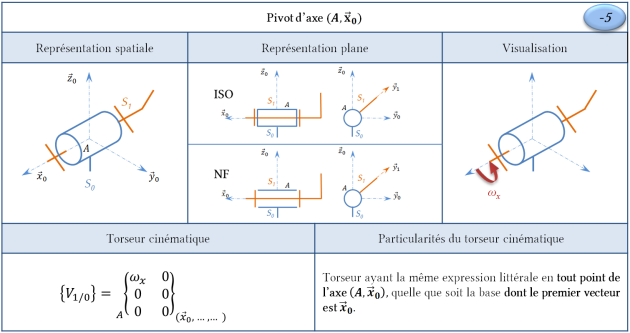
Liaison pivot glissant
Remarque : Domaine de validité du torseur cinématique
Soit un point \(B\) appartenant à l'axe \((A,\vec x_0)\). On pose \(\overrightarrow{AB}=\lambda\, \vec x_0\)avec \(\lambda \in \mathbb{R}\)
Ainsi le torseur cinématique de \(S_1/S_0\) conserve bien la même expression littérale en tout point de l'axe \((A,\vec x_0)\), quelque soit la base dont le premier vecteur est \(\vec x_0\).
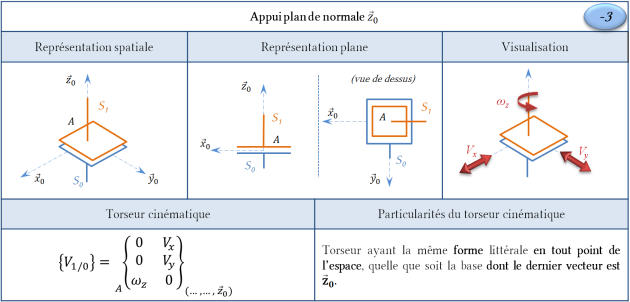
Liaison appui plan
Remarque : Domaine de validité du torseur cinématique
Soit \(B\) un point de l'espace. On pose \(\overrightarrow{AB}=\lambda \, \vec x_0 + \nu \, \vec y_0+ \mu \, \vec z_0\) avec \((\lambda,\nu,\mu) \in \mathbb{R}^3\)
Ainsi, bien que les composantes selon \(\vec x_0\) et \(\vec y_0\) de \(\overrightarrow{V_{B,S_1/S_0}}\) n'aient plus les mêmes expressions, la forme littérale du torseur est bien conservée en tout point de l'espace.
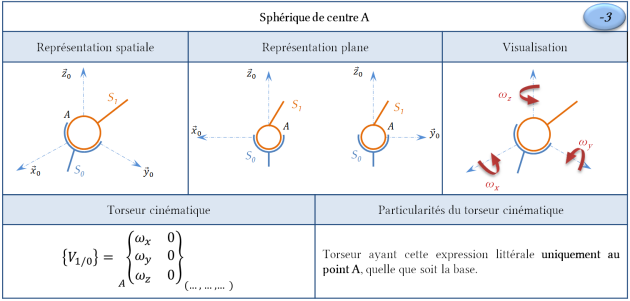
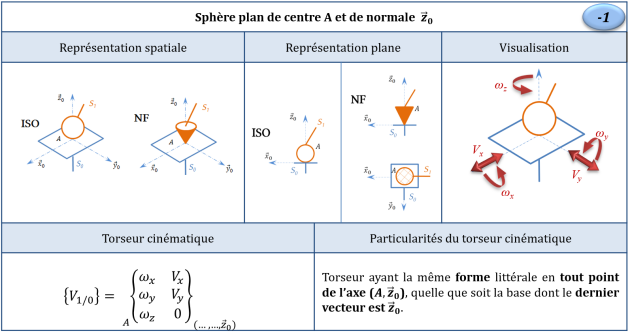
Liaison sphérique (anciennement rotule)
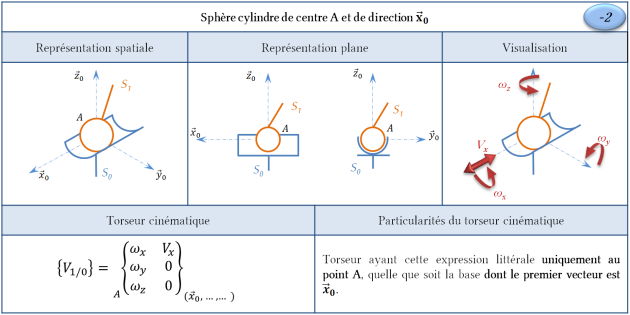
Liaison sphère cylindre (anciennement linéaire annulaire)
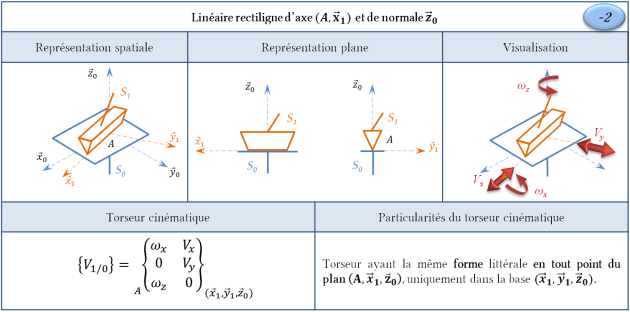
Liaison linéaire rectiligne
Remarque : Domaine de validité du torseur cinématique
Soit un point \(B\) appartenant au plan \((A,\vec x_1, \vec z_0)\), \(\overrightarrow{AB}=\lambda \, \vec x_1 + \mu \, \vec z_0\) avec \((\lambda,\mu) \in \mathbb{R}^2\)
Ainsi, bien que la composante selon \(\vec y_1\) de \(\overrightarrow{V_{B,S_1/S_0}}\) n'ait plus la même expression, la forme littérale du torseur est bien conservée en tout point du plan \((A,\vec x_1, \vec z_0)\).
Liaison sphère plan (anciennement ponctuelle)
Remarque : Domaine de validité du torseur cinématique
Soit un point \(B\) appartenant à l'axe \((A,\vec z_0)\), \(\overrightarrow{AB}=\mu \, \vec z_0\) avec \(\mu \in \mathbb{R}\)
Ainsi, bien que les composantes selon \(\vec x_0\) et \(\vec y_0\) de \(\overrightarrow{V_{B,S_1/S_0}}\) n'aient plus les mêmes expressions, la forme littérale du torseur est bien conservée en tout point de l'axe \((A,\vec z_0)\).
Liaisons composées
D'autres liaisons décrivant des mouvements simples sont définies par la norme. Elles résultent généralement de l'association de liaisons élémentaires.
Liaison encastrement
La liaison encastrement modélise les contacts entre deux solides qui n'ont aucun mouvement relatif. Tous les degrés de liberté sont bloqués.
En pratique, la liaison encastrement peut être réalisée par association de plusieurs liaisons (voir cours sur la conception des liaisons encastrement démontables) ou par soudage (voir cours sur le soudage).