Vitesse d'un point appartenant à un solide
Vecteur vitesse
Définition
Définition : Vecteur vitesse
Soit un solide \(S_1\) auquel on associe le repère \(\mathcal{R}_1(O_1, \vec x_1, \vec y_1, \vec z_1)\), en mouvement par rapport à un solide \(S_0\) auquel on associe le repère \(\mathcal{R}_0(O, \vec x_0, \vec y_0, \vec z_0)\).
Le vecteur vitesse d'un point \(M\) appartenant au solide \(S_1\) par rapport au solide \(S_0\) se calcule donc ainsi :
\(\boxed{\quad\overrightarrow{V_{M\in S_1/\mathcal{R}_0}}(t) = \left[\dfrac{d\overrightarrow{OM(t)}}{dt}\right]_{\mathcal{R}_0}\quad}\)
Remarque :
\(\overrightarrow{V_{M\in S_1/\mathcal{R}_0}}(t)\) est appelé vecteur vitesse instantané. Sa norme s'exprime en \(m/s\). Tout comme le vecteur position, il dépend du temps, et ses composantes sont des fonctions du temps.
\(\overrightarrow{V_{M\in S_1/\mathcal{R}_0}}(t)\) est tangent à la trajectoire du point \(M\in S_1\) dans \(\mathcal{R}_0\) : \(T_{M \in S_1/\mathcal R_0}\) .
On note sans distinction \(\overrightarrow{V_{M\in S_1/\mathcal{R}_0}}(t)\), \(\overrightarrow{V_{M\in S_1/S_0}}(t)\), \(\overrightarrow{V_{M\in S_1/\mathcal{R}_0}}\) ou encore \(\overrightarrow{V_{M, 1/0}}\).
Les composantes de \(\overrightarrow{V_{M\in S_1/\mathcal{R}_0}}\) peuvent s'exprimer dans n'importe quelle base.
Pour dériver le vecteur position par rapport au repère \(\mathcal{R}_0\) on peut dans un premier temps chercher à dériver ses composantes exprimée dans la base du repère \(\mathcal{R}_0\) . Nous verrons par la suite comment calculer directement la dérivée d'un vecteur par rapport à une base quelconque.
Cas du mouvement de translation
Soit \(M\) un point d'un un solide \(S_1\) en mouvement de translation rectiligne de direction \(\vec x_0\) par rapport au repère de référence \(\mathcal{R}_0\).
Nous avons vu que dans ce cas : \(\quad \forall t \in \mathbb{R}^+, \, \overrightarrow{OM}(t)= x(t) \, \vec x_0 \).
\(\begin{eqnarray*} \text{Ainsi } \, \overrightarrow{V_{M\in S_1/\mathcal{R}_0}}(t) & = & \left[\dfrac{d\overrightarrow{OM(t)}}{dt}\right]_{\mathcal{R}_0}\\ & = & \left[\dfrac{d {x(t) \,\vec x_0}}{dt}\right]_{\mathcal{R}_0}= \underbrace{\left[\dfrac{d {x(t) }}{dt}\right]_{\mathcal{R}_0}}_{=x'(t)}\vec x_0 + x(t) \, \underbrace{\left[\dfrac{d {\vec x_0}}{dt}\right]_{\mathcal{R}_0}}_{= \vec 0 \text{ car }\vec x_0 \text{ fixe dans }\mathcal{R}_0 } \end{eqnarray*}\)
\(\text{d'où } \, \boxed{\quad\overrightarrow{V_{M\in S_1/\mathcal{R}_0}}(t) = x'(t) \, \vec x_0\quad}\)
Cas du mouvement de rotation autour d'un axe fixe
\(\begin{eqnarray*} \text{Ainsi } \, \overrightarrow{V_{M\in S_1/\mathcal{R}_0}}(t) & = & \left[\dfrac{d\overrightarrow{OM(t)}}{dt}\right]_{\mathcal{R}_0}\\ & = & \left[\dfrac{d {R \, \vec e_r(t)}}{dt}\right]_{\mathcal{R}_0}= \underbrace{\left[\dfrac{d {R }}{dt}\right]_{\mathcal{R}_0}}_{= 0 \text{ car } R =cste }\vec e_r(t)+ R \, \underbrace{\left[\dfrac{d {\vec e_r(t)}}{dt}\right]_{\mathcal{R}_0}}_{\neq \vec 0 \text{ car } \vec e_r \text{ n'est pas fixe dans } \mathcal{R}_0} \end{eqnarray*}\)
\(\begin{eqnarray*} \text{Or : } \vec e_r(t) & = & \cos \theta(t)\, \vec x_0 + \sin \theta(t) \,\vec y_0\\ \text{ donc } \left[\dfrac{d {\vec e_r(t)}}{dt}\right]_{\mathcal{R}_0} & =& - \theta'(t) \, \sin \theta(t) \,\vec x_0 +\theta'(t) \, \cos \theta(t) \,\vec y_0 \\ & = & \theta'(t) \left(-\sin \theta(t) \,\vec x_0+\cos \theta(t) \,\vec y_0 \right)=\theta'(t) \, \vec e_\theta(t) \end{eqnarray*}\)
\(\text{Ainsi, } \boxed{\overrightarrow{V_{M\in S_1/\mathcal{R}_0}}(t) = R \, \theta'(t) \; \vec e_\theta}\)
Vecteur taux de rotation
Définition
Définition : Vecteur taux de rotation (ou vecteur vitesse instantané de rotation)
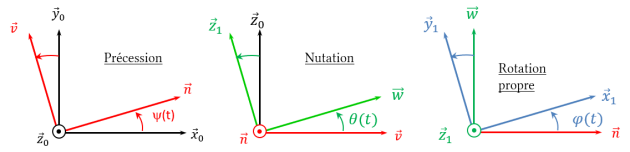
Soit un solide \(S_1\) auquel on associe le repère \(\mathcal{R}_1(O_1, \vec x_1, \vec y_1, \vec z_1)\), en mouvement par rapport à un solide \(S_0\) auquel on associe le repère \(\mathcal{R}_0(O, \vec x_0, \vec y_0, \vec z_0)\).
Les rotations entre le solide \(S_0\) et \(S_1\) sont paramétrées par les angles d'Euler :
On appelle vecteur taux de rotation ou vecteur instantané de rotation du solide \(S_1\) par rapport au solide \(S_0\) le vecteur :
Remarque :
\(\psi'(t)\), \(\theta'(t)\) et \(\varphi'(t)\) s'expriment en rad/s et correspondent aux dérivées temporelles des 3 paramètres angulaires utilisés pour orienter une base par rapport à une autre dans le cas du paramétrage d'Euler. Ils aussi parfois notés : \(\dot \psi(t)\), \(\dot \theta(t)\) et \(\dot \varphi(t)\).
On note sans distinction \(\overrightarrow{\Omega(S_1/S_0)}\), \(\overrightarrow{\Omega(\mathcal{R}_1/\mathcal{R}_0)}\), \(\overrightarrow{\Omega(1/0)}\), \(\overrightarrow{\Omega_{1/0}}\).
Le vecteur instantané de rotation est indépendant du point d'application.
On a la relation suivante : \(\overrightarrow{\Omega(S_1/S_0)}= - \, \overrightarrow{\Omega(S_0/S_1)}\)
Cas du mouvement de translation
Soit M, un point d'un un solide \(S_1\) en translation quelconque par rapport au repère de référence \(\mathcal{R}_0\). Un tel mouvement est défini par le fait que la base liée à \(S_1\) reste parallèle à elle même au cours du mouvement. Son orientation par rapport à \(\mathcal R_0\) reste donc constante. Conséquence : \(\boxed{\overrightarrow{\Omega(S_1/S_0)}=\vec 0}\)
Cas du mouvement de rotation autour d'un axe fixe
Soit \(M\), un point d'un un solide \(S_1\) en rotation autour de l'axe fixe\((O,\vec z_0)\) par rapport à au repère de référence \(\mathcal{R}_0\). Nous avons vu précédemment que dans ce cas un seul paramètre angulaire est nécessaire : l'angle \(\theta(t)\). Le vecteur taux de rotation est alors défini tel que : \(\boxed{\overrightarrow{\Omega(S_1/S_0)}=\theta'(t) \, \vec z_0}\)
Dérivation vectorielle
Définition
Fondamental : Formule de la base mobile, aussi appelée Formule de Bour.
Soient \(S_0\) et \(S_1\) deux solides en mouvements relatifs et \(\mathcal{R}_0\) et\(\mathcal{R}_1\) les repères orthonormés directs associés.
Soit \(\vec v\) un vecteur quelconque de l'espace. On note \(\overrightarrow{\Omega(S_1/S_0)}\) le vecteur taux de rotation permettant d'exprimer les rotations entre chacune des deux bases.
La dérivée d'un vecteur dans la base liée à \(\mathcal{R}_0\) calculée par la formule de la base mobile est :
Application au cas d'un solide en rotation autour d'un axe fixe
Soit \(M\), un point d'un un solide \(S_1\) en rotation autour de l'axe fixe\((O,\vec z_0)\) par rapport à au repère de référence \(\mathcal{R}_0\), paramétré par l'angle \(\theta(t)\).
Le vecteur vitesse s'écrit :
\(\overrightarrow{V_{M\in S_1/\mathcal{R}_0}}= \left[\dfrac{d \,{R \,\vec e_r(t)}}{dt}\right]_{\mathcal{R}_0} = R \,\left[\dfrac{d \,{\vec e_r(t)}}{dt}\right]_{\mathcal{R}_0} \).
Dorénavant, plutôt que de projeter le vecteur \(\vec e_r\) dans \(\mathcal{R}_0\) et de ne dériver que ses composantes, il est fortement conseillé, dans un souci d'efficacité d'utiliser la formule de la base mobile :
Ainsi :
\(\left[\dfrac{d\vec e_r}{dt}\right]_{\mathcal{R}_0} =\underbrace{\left[\dfrac{d\vec e_r}{dt}\right]_{\mathcal{R}_1}}_{= \vec 0 \text{ car }\vec e_r \text{ fixe dans }\mathcal{R}_1 }+\, \overrightarrow{\Omega(S_1/S_0)}\wedge \vec e_r \, = \, \theta'(t) \, \vec z_0 \wedge \vec e_r \,= \,\theta'(t) \, \vec e_\theta\)
On retrouve bien le fait que \(\left[\dfrac{d { \vec e_r(t)}}{dt}\right]_{\mathcal{R}_0} = \theta'(t) \; \vec e_\theta\). et donc que \(\overrightarrow{V_{M\in S_1/\mathcal{R}_0}}(t) = R \, \theta'(t) \; \vec e_\theta\)
La formule de la base mobile donne ce résultat en calculant uniquement un produit vectoriel.
Pour rappel, sans cette formule, il fallait projeter \(\vec e_r\) dans \(\mathcal R_0\), dériver par rapport au temps ses composantes, factoriser par\(\theta'(t)\) et reconnaître les composante de \(\vec e_\theta\) dans \(\mathcal R_0\).
Champ des vecteurs vitesse
Définition
Fondamental : Formule du champ des vecteurs vitesse
Soient \(A\) et \(B\) deux points appartenant à un solide \(S_1\) en mouvement par rapport à \(\mathcal R_0\). Le champ des vecteurs vitesses est déterminé ainsi :
\(\boxed{\quad \overrightarrow{V_{B\in S_1/\mathcal R_0}} =\overrightarrow{V_{A\in S_1/\mathcal R_0}} +\overrightarrow{BA} \wedge \overrightarrow{\Omega(S_1/S_0)}\quad}\)
Remarque : Utilisation du champ de vecteur
La formule du champ de vecteur vitesse est utilisée à chaque fois que la vitesse est connue en un point d'un solide (par exemple une vitesse nulle sur un axe de rotation) et qu'on veut la calculer en un autre point appartenant au même solide.
Conformément aux propriétés du produit vectoriel, cette formule s'écrit aussi :
Complément : Démonstration
Soit un solide \(S_1\) auquel on associe le repère \(\mathcal{R}_1(A, \vec x_1, \vec y_1, \vec z_1)\), en mouvement par rapport à un solide \(S_0\) auquel on associe le repère \(\mathcal{R}_0(O, \vec x_0, \vec y_0, \vec z_0)\).
Le vecteur vitesse d'un point \(B\) appartenant au solide \(S_1\) par rapport au solide \(S_0\) est donné par :
\(\overrightarrow{V_{B\in S_1/\mathcal{R}_0}} = \left[\dfrac{d\overrightarrow{OB(t)}}{dt}\right]_{\mathcal{R}_0}\)
D'après la relation de Chasles, \(\overrightarrow{OB(t)} = \overrightarrow{OA(t)} + \overrightarrow{AB(t)}\) donc :
\(\overrightarrow{V_{B\in S_1/\mathcal{R}_0}} = \left[\dfrac{d \left(\overrightarrow{OA(t)} + \overrightarrow{AB(t)}\right)}{dt}\right]_{\mathcal{R}_0}=\underbrace{\left[\dfrac{d\overrightarrow{OA(t)}}{dt}\right]_{\mathcal{R}_0}}_{(1)}+\underbrace{\left[\dfrac{d\overrightarrow{AB(t)}}{dt}\right]_{\mathcal{R}_0}}_{(2)}\)
(1) : par définition du vecteur vitesse : \(\left[\dfrac{d\overrightarrow{OA(t)}}{dt}\right]_{\mathcal{R}_0}=\overrightarrow{V_{A\in S_1/ \mathcal R_0}}\)
(2) : d'après la formule de la base mobile : \(\left[\dfrac{d\overrightarrow{AB(t)}}{dt}\right]_{\mathcal{R}_0}=\left[\dfrac{d\overrightarrow{AB(t)}}{dt}\right]_{\mathcal{R}_1} + \overrightarrow{\Omega(S_1/S_0)} \wedge \overrightarrow{AB(t)}\)
Or : \(\left[\dfrac{d\overrightarrow{AB(t)}}{dt}\right]_{\mathcal{R}_1}=\vec 0\) car \(B\) est fixe dans le repère \(\mathcal{R}_1\) (d'origine \(A\)) lié à \(S_1 \)supposé indéformable.
Donc au final : \(\overrightarrow{V_{B\in S_1/\mathcal{R}_0}} =\overrightarrow{V_{A\in S_1/\mathcal{R}_0}} + \overrightarrow{\Omega(S_1/S_0)}\wedge \overrightarrow{AB}=\overrightarrow{V_{A\in S_1/\mathcal{R}_0}} +\overrightarrow{BA} \wedge \overrightarrow{\Omega(S_1/S_0)}\)
Cas du mouvement de translation
Soit M, un point d'un un solide \(S_1\) en translation quelconque par rapport au repère de référence \(\mathcal{R}_0\).
\(\quad\overrightarrow{V_{M\in S_1/\mathcal{R}_0}}(t) = x'(t) \, \vec x_0\quad\)
Soit N un autre point quelconque de \(S_1\). D'après la formule du champ des vecteurs vitesse :
\(\overrightarrow{V_{N\in S_1/\mathcal{R}_0}} =\overrightarrow{V_{M\in S_1/\mathcal{R}_0}} +\overrightarrow{NM} \wedge \overrightarrow{\Omega(S_1/S_0)}\).
Or pour un mouvement de translation : \(\overrightarrow{\Omega(S_1/S_0)}=\vec 0\), donc :
\(\overrightarrow{V_{N\in S_1/\mathcal{R}_0}} =\overrightarrow{V_{M\in S_1/\mathcal{R}_0}}\)
Fondamental : Conclusion : Mouvement de translation
A tout instant t, tous les points d'un solide \(S_1\) en mouvement de translation par rapport à un repère \(R_0\) ont le même vecteur vitesse. On dit que le champ des vitesses est uniforme.
Cas du mouvement de rotation autour d'un axe fixe
Soit un solide \(S_1\) en mouvement de rotation autour de l'axe fixe\((O,\vec z_0)\) par rapport au repère de référence \(\mathcal{R}_0\) lié à \(S_0\), et paramétré par l'angle \(\theta(t)\).
Par définition du mouvement de rotation : \(\overrightarrow{V_{O\in S_1/\mathcal{R}_0}}= \, \vec 0\).
Soit M un point du solide \(S_1\) situé à un rayon R de l'axe de rotation. D'après la formule du champ des vecteurs vitesse :
\(\begin{eqnarray*} \overrightarrow{V_{M\in S_1/\mathcal{R}_0}} & =& \overrightarrow{V_{O\in S_1/S_0}} +\overrightarrow{MO} \wedge \overrightarrow{\Omega(S_1/S_0)}\\ & = & \vec 0 -R \, \vec e_r \wedge \theta'(t)\, \vec z_0\\ & = & R \, \theta'(t) \, \vec e_\theta = R \, \omega_{1/0} \, \vec e_\theta\end{eqnarray*}\).
On retrouve bien le résultat établi précédemment, mais cette fois-ci, le calcul ne nécessite pas de dérivation, uniquement un produit vectoriel.
Fondamental : Conclusion : Mouvement de rotation
Pour un mouvement de rotation autour d'un axe fixe,
En tout point de l'axe de rotation, la vitesse est nulle : \(\overrightarrow{V_{O\in S_1/\mathcal{R}_0}}= \, \vec 0\) ;
\(\overrightarrow{V_{M\in S_1/\mathcal{R}_0}} =\overrightarrow{\Omega(S_1/S_0)} \wedge \overrightarrow{OM}\) donc les vecteurs vitesse sont perpendiculaires aux « rayons » et à l'axe de rotation ;
La norme des vecteurs vitesse est proportionnelle à la distance à l'axe et au taux de rotation. Si M est à une distance \(R\) de l'axe : \(\Vert \, \overrightarrow{V_{M\in S_1/\mathcal{R}_0}} \,\Vert = R \, | \omega_{1/0} |\).