Changement de base [C03_P1 : Cinématique du solide]

Changement de base

Passage de la base cylindrique à la base cartésienne

Le passage d'une base à une autre n'est qu'une histoire de projection de vecteurs. Il est déconseillé de tenter ces projections à partir d'une vue 3D : certaines perspectives sont trompeuses, les angles peuvent être représentés négativement et peuvent avoir des valeurs proches de 45° (risque de confusion sinus/cosinus).

Les projections doivent impérativement s'appuyer sur des figures planes de changement de base : vues 2D définissant un seul angle à la fois. Cet angle doit être positif, de valeur environ 30°.

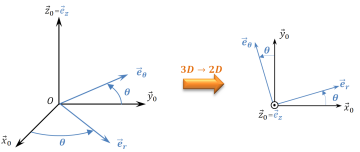
Utilisation d'une figure plane de changement de base

En s'appuyant sur la figure plane, on peut écrire les relations entre les différents vecteurs :

\[\left \{ \begin{array}{l} \vec e_r=\cos \theta \, \vec x_0 + \sin \theta \, \vec y_0 \\ \vec e_\theta = - \sin \theta \, \vec x_0 + \cos \theta \, \vec y_0 \\ \vec e_z = \vec z_0 \end{array} \right . \quad \text{ ou encore } \quad \left \{ \begin{array}{l} \vec x_0=\cos \theta \, \vec e_r - \sin \theta \, \vec e_\theta\\ \vec y_0 = \sin \theta \, \vec e_r + \cos \theta \, \vec e_\theta \\ \vec z_0 = \vec e_z \end{array} \right .\]

Remarque : Cas d'un solide en rotation autour d'un axe fixe

Nous avons vu dans la partie précédente que dans le cas d'un solide en rotation autour d'un axe fixe, le vecteur position est : \(\overrightarrow{OM}(t)= R \, \vec e_r(t)\)

Connaissant désormais les composantes de la base cylindriques dans la base cartésiennes, plus précisément celle du vecteur \(\vec e_r\) , on peut exprimer le vecteur position dans la base cartésienne en fonction des paramètres cylindriques du mouvement : \(\overrightarrow{OM}(t)= \, R \, \vec e_r(t) \, = \, R \times (\cos \theta \, \vec x_0 + \sin \theta \, \vec y_0 )= \quad {\vphantom{\left\{\begin{array}{ccc}a\\b\\c\\\end{array}\right\}}}_{(\vec x_0, \vec y_0, \vec z_0)}{ } \left | \begin{array}{c}R \,\cos \theta(t)\\ R \, \sin \theta(t) \\0 \end{array} \right .\quad\)

Cas général : les angles d'Euler

Dans le cas général, l'orientation d'une base par rapport à une autre peut nécessiter jusqu'à 3 paramètres géométriques angulaires. Le paramétrage d'Euler permet de passer d'une base initiale \(B_i : (\vec x_i,\vec y_i,\vec z_i)\) à une base quelconque \(B_F : (\vec x_F,\vec y_F,\vec z_F)\) en utilisant trois rotations précisément définies :

1^ère rotation , la précession :
\((\vec x_i,\vec y_i,\vec z_i) \overset{\text{Rotation }(\psi,\vec z_i)}{\longrightarrow} (\vec n,\vec v,\vec z_i)\)

2^ème rotation , la nutation :
\((\vec n,\vec v,\vec z_i) \overset{\text{Rotation }(\theta,\vec n)}{\longrightarrow} (\vec n,\vec w,\vec z_F)\)

3^ème rotation , la rotation propre :
\((\vec n,\vec w,\vec z_F) \overset{\text{Rotation }(\varphi,\vec z_F)}{\longrightarrow} (\vec x_F,\vec y_F,\vec z_F)\)

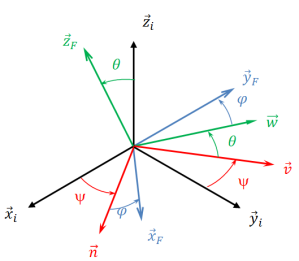
Les trois angles d'Euler \(\psi, \theta\) et \(\varphi\) portent le noms des rotations correspondantes :

\(\psi\) : angle de precession ;

\(\theta\) : angle de nutation ;

\(\varphi\) : angle de rotation propre.

Pour exprimer les composantes des vecteurs de la base \(B_F : (\vec x_F,\vec y_F,\vec z_F)\) en fonction des vecteurs de la base \(B_i : (\vec x_i,\vec y_i,\vec z_i)\), on réalise les 3 figures planes de changement de base. On détermine alors par projections successives et pour chaque rotation les composantes des vecteurs de la base d'arrivée dans la base de départ.

Précession :

\(\left \{\begin{array}{l}\vec n =\cos \psi \, \vec x_i + \sin \psi \, \vec y_i \\\vec v = - \sin \psi \, \vec x_i + \cos \psi \, \vec y_i \\\vec z_i \end{array}\right .\)

Nutation :

\(\left \{\begin{array}{l}\vec n \\ \vec w= \cos \theta \, \vec v + \sin \theta \, \vec z_i \\ \vec z_F = - \sin \theta \, \vec v + \cos \theta \, \vec z_i \\ \end{array}\right .\)

Rotation propre :

\(\left \{\begin{array}{l} \vec x_F= \cos \varphi \, \vec n + \sin \varphi \, \vec w \\ \vec y_F = - \sin \varphi\, \vec n + \cos \varphi \, \vec w \\\vec z_F \end{array}\right .\)

Au final, on obtient :

\[\boxed{ \, \vec x_F = {\vphantom{\left\{\begin{array}{ccc}a\\b\\c\\\end{array}\right\}}}_{(\vec x_i, \vec y_i, \vec z_i)}{ } \left | \begin{array}{c} \cos \varphi \, \cos \psi - \sin \varphi \, \cos \theta \, \sin \psi \\ \cos \varphi \, \sin \psi + \sin \varphi \, \cos \theta \, \cos \psi \\ \sin \varphi \, \sin \theta \end{array} \right . \, } \text{ , } \, \boxed{ \vec y_F = {\vphantom{\left\{\begin{array}{ccc}a\\b\\c\\\end{array}\right\}}}_{(\vec x_i, \vec y_i, \vec z_i)}{ } \left | \begin{array}{c} -\sin \varphi \, \cos \psi - \cos \varphi \, \cos \theta \, \sin \psi \\ -\sin \varphi \, \sin \psi + \cos \varphi \, \cos \theta \, \cos \psi \\ \cos \varphi \, \sin \theta \end{array} \right . \, } \]

\[\text{ et } \, \boxed{ \vec z_F = {\vphantom{\left\{\begin{array}{ccc}a\\b\\c\\\end{array}\right\}}}_{(\vec x_i, \vec y_i, \vec z_i)}{ } \left | \begin{array}{c} \sin \theta \, \sin \psi \\ -\sin \theta \, \cos \psi \\ \cos \theta \end{array} \right . \, }\]

Ce résultat n'est pas à apprendre, mais la démarche permettant de le retrouver doit être maîtrisée.