Lois de mouvement - Lois horaires

Mouvement de translation rectiligne

Dans le cas d'un solide \(S\) en mouvement de translation rectiligne de direction \(\vec x_0\) dans le référentiel de référence \(\mathcal{R}_0(O,\vec x_0, \vec y_0, \vec z_0)\) , un seul paramètre \(x(t)\) suffit à connaître la position d'un point \(M\) lié à \(S\) à tout instant :

\(\left \{ \begin{array}{l} \overrightarrow{OM}(t) = x(t)\, \vec x_0\\ \overrightarrow{V_{M \in S /\mathcal R_0} }(t) = x'(t) \, \vec x_0\\ \overrightarrow{\Gamma_{M \in S /\mathcal R_0} }(t) = x''(t) \, \vec x_0 \quad\textit{, par définition du vecteur accélération.}\end{array} \right .\)

Dans le cas d'un accélération constante, \(x''(t)=cte=a_0\) , on peut déterminer par intégration la vitesse et la position du point \(M\) et établir les lois horaires du mouvement :

\[\boxed { \quad \forall t \geq 0, \, \left \{ \begin{array}{l} x''(t) = x''_0 = a_0 =cte \\ x'(t)= v(t) = a_0 \times t+v_0 \\ x(t) = a_0 \times \frac{t^2}{2}+ v_0 \times t+x_0 \end{array} \right . \quad}\]

Remarque

  1. \(v_0\) et \(x_0\) représentent respectivement la vitesse et la position initiales du point M, soit à l'instant à t=0 s.

  2. Si \(a_0=cte \neq 0 \,m/s^2\), on parle de mouvement de translation rectiligne uniformément varié (accéléré ou décéléré).

  3. Si \(a_0= 0 \,m/s^2\), on parle de mouvement de translation rectiligne uniforme.

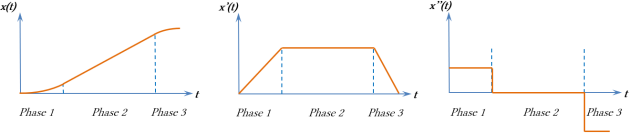
Les lois horaires permettent l'étude de la translation d'un solide dans le cadre d'une loi de vitesse en trapèze cumulant :

  • Phase 1 : mouvement de translation rectiligne uniformément accéléré.

  • Phase 2 : mouvement de translation rectiligne uniforme.

  • Phase 3 : mouvement de translation rectiligne uniformément décéléré.

L'étude d'un mouvement commençant à \(t=t_i>0\) (cas des phases 2 et 3 par exemple) nécessite un changement de variable dans les équations horaires. Les équations horaires deviennent :

\[\boxed { \quad \forall t \geq t_i, \, \left \{\begin{array}{l} x''(t) = a_i = cte\\ x'(t) = a_i \times (t-t_i)+{v_i}_0 \\ x(t) = a_i \times \frac{(t-t_i)^2}{2}+ {v_i}_0 \times (t-t_i)+{x_i}_0 \end{array}\right .\quad}\]

où \({v_i}_0\) et \({x_i}_0\) représentent respectivement la vitesse et la position initiales du point \(M\) pour la phase étudiée, soit à l'instant à \(t=t_i\).

Mouvement de rotation autour d'un axe fixe

Dans le cas d'un solide S en mouvement de rotation autour d'un axe fixe \((O_0,\vec z_0)\) par rapport au référentiel de référence \(\mathcal{R}_0(O,\vec x_0, \vec y_0, \vec z_0)\), on rappelle :

\[\forall M \in S \, \left \{ \begin{array}{l} \overrightarrow{OM}(t)= R \, \vec e_r(t) \\ \overrightarrow{V_{M\in S_1/\mathcal{R}_0}}(t) = R \, \theta'(t) \; \vec e_\theta \\ \overrightarrow{\Gamma_{M\in S_1/S_0}}(t) = R \, \theta''(t) \, \vec e_\theta \, - \, R \, \theta'(t)^2 \, \vec e_r \end{array} \right . \]

Ainsi, un seul paramètre \(\theta(t)\) (et ses dérivées) suffit à connaître les position, vitesses et accélération d'un point M lié à S à tout instant. Par analogie avec le mouvement rectiligne, on peut établir les équations horaires du mouvement :

\[\boxed { \quad \forall t \geq t_i, \, \left \{ \begin{array}{l} \theta''(t) = \theta''_{i0} = cte \\ \theta'(t) = \theta''_{i0} \times (t-t_i)+\theta'_{i0} \\ \theta(t) = \theta''_{i0} \times \frac{(t-t_i)^2}{2}+ \theta'_{i0} \times (t-t_i)+\theta_{i0} \quad \end{array} \right . \quad}\]

Remarque

  1. \(\theta'_{i0}\) et \(\theta_{i0}\) représentent respectivement la vitesse angulaire et la position angulaire initiales du point M pour la phase étudiée, soit à l'instant à \(t=t_i\). \(\theta''(t)\) représente l'accélération angulaire en \(rad/s^2\).

  2. On note souvent \(\theta' (t)= \omega(t)\) pour la vitesse angulaire. Ainsi, \(\theta''(t) =\omega'(t)\) , \(\theta''_{i0} = \omega'_{i0}\) et \(\theta'_{i0} = \omega_{i0}\).

  3. Si \(\theta''_{i0} = \omega'_{i0}=cte \neq 0 \, rad/s^2\), on parle de mouvement de rotation uniformément varié (accéléré ou décéléré).

  4. Si \(\theta''_{i0} = \omega'_{i0}= 0 \, rad/s^2\), on parle de mouvement de rotation uniforme.

  5. Tout comme dans le cas du mouvement de translation, ces équations permettent l'étude des mouvement avec une loi de vitesse (angulaire) dite en trapèze.