Mouvements et Référentiel d'étude
Définition
La notion de mouvement associe le concept de variation de la position du solide observé à celui d'écoulement du temps. Cette notion est relative : elle n'a de sens que si on définit préalablement le solide dont on étudie le mouvement et le solide de référence par rapport auquel ce mouvement a lieu.
En cinématique, et plus généralement en mécanique, l'étude des mouvements des solides et des points qui les constituent s'effectue dans un référentiel d'étude.
Définition : Référentiel d'étude
Un référentiel d'étude est l'ensemble formé par un repère spatial de référence et un repère temporel :
le repère spatial de référence est défini par un point Origine et une base (généralement orthonormée directe) liée à l'espace d'observation ; On le note par exemple :\(\mathcal{R}_0(O,\vec x_0, \vec y_0, \vec z_0)\)
le repère temporel est défini par un instant Origine (\(t=t_0\)) et une unité de temps (la seconde).
Un fois le référentiel d'étude défini, on associe à chaque solide un repère spatial orthonormé et direct. Etudier les mouvement d'un solide indéformable revient alors à étudier les déplacements du répère associé à ce solide par rapport au repère de référence. Dans un espace en 3 dimensions, il existe 6 mobilités ou degrés de liberté possibles :
3 translations : \(T_x,T_y\) et \(Tz\)
3 rotations : \(Rx,Ry\) et \(Rz\)
Mouvement de translation
Définition : Mouvement de translation
On dit qu'un solide \(S_1\) est en mouvement de translation par rapport au repère de référence \(\mathcal R_0\) si au cours du mouvement (par rapport à \(\mathcal R_0\)) , un repère \(\mathcal R_1(O_1,\vec x_1, \vec y_1, \vec z_1)\) lié au solide \(S_1\) reste constamment parallèle à lui-même.
Exemple : Lame de scie sauteuse
Remarque : Liaison glissière
Un mouvement de translation rectiligne (l'origine du repère se déplace le long d'un ligne droite) de direction \(\vec x_0\) est schématisé par une liaison glissière de direction \(\vec x_0\) , dont le symbole normalisé est :
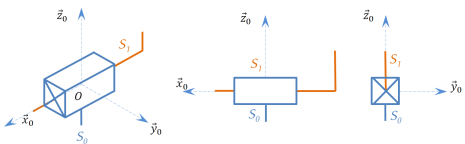
Mouvement de rotation autour d'un axe fixe
Définition : Mouvement de rotation autour d'un axe fixe
Le mouvement d'un solide \(S_1\) par rapport au repère de référence \(\mathcal{R}_0\) est une rotation autour d'un axe fixe s'il existe au moins deux points distincts \(A\) et \(B\) de \(S_1\), immobiles par rapport à \(\mathcal{R}_0\) au cours du mouvement.
La droite \((AB)\) est appelée axe de rotation. Tous les points de l'axe \((AB)\) appartenant au solide \(S_1\) sont fixes par rapport au repère \(\mathcal{R}_0\).
Exemple : Pales d'éolienne
Remarque : Liaison pivot
Un mouvement de rotation autour d'un axe \((O, \vec z_0)\) entre deux solides \(1\) et \(2\) est schématisé par une liaison pivot d'axe \((O,\vec z_0)\) dont le symbole normalisé est :