Torseur des petits déplacements
Définition
La prise en compte des jeux lors du contact entre deux solides \(1\) et \(2\) autorise des mouvements supplémentaires de faible amplitude : on parle de petits déplacements. Ces petits déplacements autorisés par la liaison réelle (\(\neq\) liaison parfaite) sont modélisés par un torseur : le torseur des petits déplacements.
Définition : Torseur des petits déplacements
On définit donc le torseur des petits déplacements du solide 2 par rapport au solide 1 :
La résultante \(\overrightarrow{\delta \theta_{ 2/1}}\) est appelée vecteur petite rotation de 2 par rapport à 1.
Le moment \(\overrightarrow{\delta u_{A \in 2/1}}\) est appelé vecteur petit déplacement du point A appartenant à 2 par rapport à 1.
Complément : Démonstration
Les éléments de réduction peuvent être obtenus à partir de ceux du torseur cinématique \(\{\mathcal V _{2/1}\}\).
Soient un solide 2 en mouvement par rapport à un autre solide 1 et \(A\) et \(B\) sont deux points quelconques appartenant à 2.
On a : \(\overrightarrow{V_{B \in 2/1}} =\overrightarrow{V_{A \in 2/1}} + \overrightarrow{BA} \wedge \overrightarrow{\Omega_{ 2/1}}\)
Soit \(dt\) un intervalle de temps élémentaire. On peut alors écrire :
\(dt.\overrightarrow{V_{B \in 2/1}} =dt.\overrightarrow{V_{A \in 2/1}} + dt.\overrightarrow{BA} \wedge \overrightarrow{\Omega_{ 2/1}}\)
On pose alors : \(\overrightarrow{\delta u_{B \in 2/1}} = dt.\overrightarrow{V_{B \in 2/1}}\)et \(\overrightarrow{\delta \theta_{ 2/1}} = dt.\overrightarrow{\Omega_{ 2/1}}\)
Ce qui revient à dire que les points \(A\) et \(B\) se déplacent en ligne droite (voir figure ci-dessous). Ce n'est pas vrai pour un mouvement de grande amplitude, mais si le déplacement du solide est faible, cette approximation est très pertinente.
On a donc la relation : \(\overrightarrow{\delta u_{B \in 2/1}} =\overrightarrow{\delta u_{A \in 2/1}} + \overrightarrow{BA} \wedge \overrightarrow{\delta \theta_{ 2/1}}\)
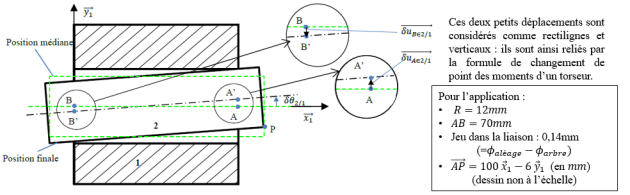
Application au guidage cylindrique
Objectif : déterminer l'angle d'inclinaison de l'arbre \(\delta \theta_{ 2/1}=\Vert \, \overrightarrow{\delta \theta_{ 2/1}} \, \Vert\) ainsi que le vecteur petit déplacement du point P \(\overrightarrow{\delta u_{P \in 2/1}}\) .
Calcul de \(\delta \theta_{ 2/1}\) :
La relation entre les petits déplacements de A et de B s'écrit :
\(\overrightarrow{\delta u_{B \in 2/1}} =\overrightarrow{\delta u_{A \in 2/1}} + \overrightarrow{BA} \wedge \overrightarrow{\delta \theta_{ 2/1}} \quad \text{avec } \quad \left \{ \begin{array}{ l} \overrightarrow{\delta u_{A \in 2/1}}=0,07 \vec y_1 \quad \textit{(en mm)}\\ \overrightarrow{\delta u_{B \in 2/1}}=-0,07 \vec y_1 \quad \textit{(en mm)}\\ \overrightarrow{BA}=70 \vec x_1\quad \textit{(en mm)}\end{array} \right .\)
Ce qui donne : \(\overrightarrow{\delta \theta_{ 2/1}}=0,002\vec z_1\) (en radians) , c'est-à-dire : \(\boxed{\delta \theta_{ 2/1}=0,11^{\circ}}\)
Pour le déplacement du point P, on se sert du petit déplacement du point A qui peut être déterminé à partir du jeu fonctionnel de la liaison :
\(\overrightarrow{\delta u_{P \in 2/1}} =\underbrace{\overrightarrow{\delta u_{A \in 2/1}}}_{0,07 \vec y_1}+ \underbrace{\overrightarrow{PA}}_{-100 \vec x_1+6 \vec y_1} \wedge \underbrace{\overrightarrow{\delta \theta_{ 2/1}}}_{0,002 \vec z_1}=\boxed{0,27 \,\vec y_1 + 0,012 \,\vec x_1}\quad \textit{(en mm)}\)