C04 : Modéliser la cinématique des mécanismes

Bien que la modélisation cinématique s'effectue dans le cadre des liaisons parfaites, le cas des contacts cylindriques fait souvent figure d'exception. En effet, afin d'autoriser certaines mobilités relatives (et donc éviter d'avoir un ajustement serré), la liaison réelle est conçue avec un jeu fonctionnel radial entre l'arbre et l'alésage. Ce jeu n'est évidemment pas sans conséquence dans la modélisation cinématique.

La figure suivante présente un arbre 1 guidé dans un alésage 0. On est tenté de dire que la modélisation d'un tel assemblage est une liaison pivot glissant. Et pourtant...

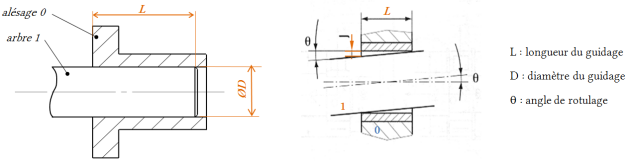
Le jeu radial Jr (\(Jr = Ø_\textit{Alésage}-Ø_\textit{arbre}\)) induit un angle de rotulage \(\theta\). Cet angle caractérise la précision du positionnement de l'axe du guidage.

Le problème est de savoir à partir de quel angle de rotulage \(\theta\) on passe de la modélisation par une liaison pivot glissant à la modélisation par un liaison sphére-cylindre (ou d'une liaison pivot à une liaison sphèrique s'il y a des arrêts axiaux). Un résultat empirique fonction du rapport \(\frac L D\) permet de choisir la liaison.

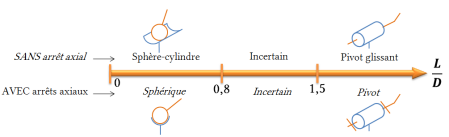
Cela signifie que pour \(\frac L D \leq 0,8\), on ne néglige plus les degrés de libertés de rotation autour des axes orthogonaux à l'axe du guidage. On choisit d'en tenir compte dans la modélisation.

La zone qui s'étend de 0,8 à 1,5 est discutable et requière un regard particulier sur la qualité de réalisation, le choix des matériaux, les états de surface, etc.