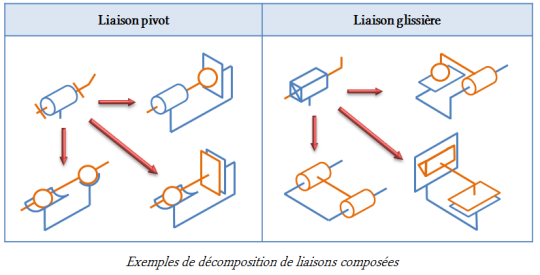
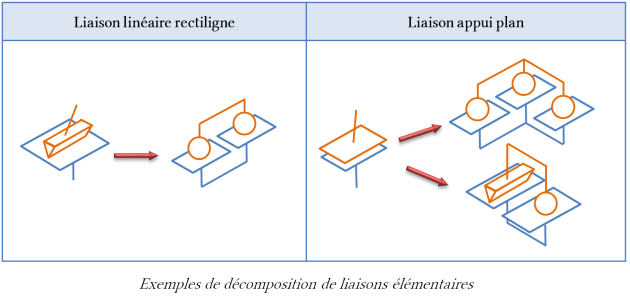
Association de liaisons [C04 : Modéliser la cinématique des mécanismes]

Association de liaisons

Lorsqu'on rencontre une disposition de liaisons en série ou en parallèle, la liaison équivalente est identifiée en calculant son torseur cinématique. Si la liaison obtenue est normalisée, on peut alors simplifier la modélisation en remplaçant les deux liaisons initiales par une liaison unique.

Liaisons en série

Fondamental : Association de liaisons en série

La liaison équivalente entre 0 et 2 se détermine par composition des torseurs cinématiques :

\[ \boxed{ \quad \left \{ \mathcal V _{L_{eq}} \right \} =\left \{ \mathcal V _{L_{2/1}} \right \} +\left \{ \mathcal V _{L_{1/0}} \right \} \quad}\]

Attention :

La simplification de liaisons en série ne doit pas être systématique. Elle n'est pertinent que lorsque la classes d'équivalente intermédiaire (qui disparaît donc de la modélisation) ne présente pas d'intérêt cinématique.

Exemple : Pompe à pistons axiaux

L'étude de la pompe à pistons axiaux met en évidence des liaisons en série entre les pistons, les patins et le plan incliné. Les patins permettent de répartir les efforts exercés par les pistons sur le plan incliné afin de diminuer la pression de contact pouvant endommager localement les pièces. En effet, sans eux, le contact entre un piston et le plan incliné serait ponctuel alors qu'ici, ce contact ponctuel est remplacé par deux contacts surfaciques : l'un sphérique, l'autre plan.

D'un point de vue cinématique, on peut montrer que ces patins n'ont pas d'intérêt. Pour s'en convaincre, on peut calculer la liaison équivalente à l'association en série d'une liaison sphérique et d'une liaison appui plan. Le torseur cinématique de la liaison équivalente s'obtient en additionnant celui de la liaison sphérique et celui de la liaison appui-plan en s'assurant qu'ils sont exprimés au même point (et dans la même base si l'on utilise les notations colonnes) :

\[\begin{matrix} \left \{ \mathcal V _{L_{eq}} \right \} = \left \{ \mathcal V _{L_{2/1}} \right \} +\left \{ \mathcal V _{L_{1/0}} \right \} & \Leftrightarrow & \quad \left \{ \mathcal V _{L_{eq}} \right \} & = & {\vphantom{\begin{Bmatrix} \omega_x & V_x \\ \omega_y & V_y \\ \omega_z & V_z\end{Bmatrix} }}_{A} \begin{Bmatrix} \omega_{x}^{21} & 0 \\ \omega_{y}^{21}& 0 \\ \omega_{z}^{21} & 0 \end{Bmatrix} _{(\vec {x_1}, \vec {y_1}, \vec {z_1})} + {\vphantom{\begin{Bmatrix} \omega_x & V_x \\ \omega_y & V_y \\ \omega_z & V_z\end{Bmatrix} }}_{A} \begin{Bmatrix} \omega_{x}^{10} & 0\\ 0 & V_{y}^{10}\\ 0 & V_{z}^{10}\end{Bmatrix} _{(\vec {x_1}, \vec {y_1}, \vec {z_1})}& \\ & \Leftrightarrow & \quad \left \{ \mathcal V _{L_{eq}} \right \} & = & {\vphantom{\begin{Bmatrix} \omega_x & V_x \\ \omega_y & V_y \\ \omega_z & V_z\end{Bmatrix} }}_{A} \begin{Bmatrix} \omega_{x}^{21}+ \omega_{x}^{10} & 0 \\ \omega_{y}^{21} & V_{y}^{10} \\ \omega_{z}^{21} & V_{z}^{10}\end{Bmatrix} _{(\vec {x_1}, \vec {y_1}, \vec {z_1})} \\ \end{matrix}\]

Ainsi \(\left \{ \mathcal V _{L_{eq}} \right \}\) est de la forme : \({\vphantom{\begin{Bmatrix} \omega_x & V_x \\ \omega_y & V_y \\ \omega_z & V_z\end{Bmatrix} }}_{A}\begin{Bmatrix} \omega_{x_{eq}} & 0 \\ \omega_{y_{eq}} & V_{y_{eq}} \\ \omega_{z_{eq}} & V_{z_{eq}}\end{Bmatrix} _{(\vec {x_1}, \vec {y_1}, \vec {z_1})}\)

Conclusion : la liaison équivalente du piston \(2\) par rapport au plan incliné \(0\) est donc une liaison sphère plan de centre \(A\) et de normale \(\vec x_1\).

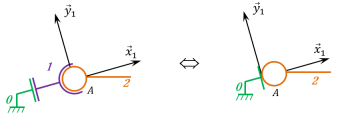
Ainsi, dans un objectif purement cinématique d'étude des mouvements, les patins peuvent être omis de l'étude et on remplace alors dans le graphe des liaisons l'association en série des deux liaisons par une seule liaison sphère plan.

Attention : Addition de deux torseurs

Pour pouvoir additionner les composantes de deux torseurs, ceux-ci doivent être réduits au même point (et leurs composantes exprimées dans la même base lors de l'utilisation des notations en colonnes). Dans l'exemple ci-dessus, le torseur de la liaison appui plan ayant la même forme en tout point de l'espace, on peut choisir de l'exprimer directement au point A. Mais bien souvent, le calcul d'une liaison équivalente nécessite de déplacer un des deux torseurs. Dans ce cas il est plus efficace de déplacer le torseur ayant le moins de composantes non nulles (= torseur ayant le plus de composantes nulles) afin de simplifier les calculs.

Liaisons en parallèle

Fondamental : Association de liaisons en parallèle

La liaison équivalente entre \(1\) et \(0\) doit autoriser les mêmes mouvements que les deux liaisons initiales. Le torseur de la liaison équivalente se détermine alors en égalisant les torseurs cinématiques :

\[ \boxed{ \quad \left \{ \mathcal V _{L_{eq}} \right \} =\left \{ \mathcal V _{L_{1/0}} \right \} = \left \{ \mathcal V _{L'_{1/0}} \right \} \quad}\]

Exemple : Micromoteur de modélisme

Le guidage en rotation du vilebrequin par rapport au carter est assuré par deux liaisons élémentaires en parallèle : un liaison pivot glissant permettant de définir l'axe de rotation et une liaison appui plan dont la normale correspond à l'axe de la liaison pivot glissant afin de définir la position axial du vilebrequin par rapport au carter.

La liaison équivalente entre \(1\) et \(2\) doit autoriser les mêmes mouvements que les deux liaisons en parallèle :

\[\begin{matrix} \left \{ \mathcal V _{L_{eq}} \right \} =\left \{ \mathcal V _{L_{1/0}} \right \} = \left \{ \mathcal V _{L'_{1/0}} \right \} \\ \text{Or : } \left \{ \mathcal V _{L_{1/0}} \right \} = {\vphantom{\begin{Bmatrix} \omega_x & V_x \\ \omega_y & V_y \\ \omega_z & V_z\end{Bmatrix} }}_{O} \begin{Bmatrix} 0 & V_{x}\\ 0 & V_{y} \\ \omega_{z} & 0\end{Bmatrix} _{(\vec {x_0}, \vec {y_0}, \vec {z_0})} \text{ et } \left \{ \mathcal V _{L'_{1/0}} \right \} = {\vphantom{\begin{Bmatrix} \omega_x & V_x \\ \omega_y & V_y \\ \omega_z & V_z\end{Bmatrix} }}_{O} \begin{Bmatrix} 0 & 0\\ 0 & 0 \\ \omega'_{z} & V'_{z}\end{Bmatrix} _{(\vec {x_0}, \vec {y_0}, \vec {z_0})} \\ \text{Donc, } \left \{ \mathcal V _{L_{1/0}} \right \} = \left \{ \mathcal V _{L'_{1/0}} \right \} \Leftrightarrow \left \{ \begin{array}{r c l} \omega_{z} & = & \omega'_{z} \\ V_{x} & = & 0 \\ V_{y} & = & 0 \\ V'_{z} & = & 0 \\ \end{array} \right . \\ \text{Soit : } \boxed{ \left \{ \mathcal V _{L_{eq}} \right \} = {\vphantom{\begin{Bmatrix} \omega_x & V_x \\ \omega_y & V_y \\ \omega_z & V_z\end{Bmatrix} }}_{O} \begin{Bmatrix} 0 & 0\\ 0 & 0 \\ \omega'_{z} & 0 \end{Bmatrix} _{(\vec {x_0}, \vec {y_0}, \vec {z_0})} } \end{matrix}\]

Conclusion : la liaison équivalente du vilebrequin \(1\) par rapport au carter \(0\) est donc une liaison pivot d'axe \((O,\vec z_0)\).

Attention : Egalisation de deux torseurs

Pour pouvoir égaliser les composantes de deux torseurs, ceux-ci doivent être réduits au même point (et leurs composantes exprimées dans la même base lors de l'utilisation des notations en colonnes). Dans l'exemple ci-dessus, le torseur de la liaison appui plan ayant la même forme en tout point de l'espace, on peut choisir de l'exprimer directement en un point de l'axe de la liaison pivot, par exemple au point O. Mais bien souvent, le calcul d'une liaison équivalente nécessite de déplacer un des deux torseurs. Dans ce cas il est plus efficace de déplacer le torseur ayant le moins de composantes non nulles (= torseur ayant le plus de composantes nulles) afin de simplifier les calculs.