Graphe des liaisons (ou graphe de structure)
Définition : Graphe des liaisons
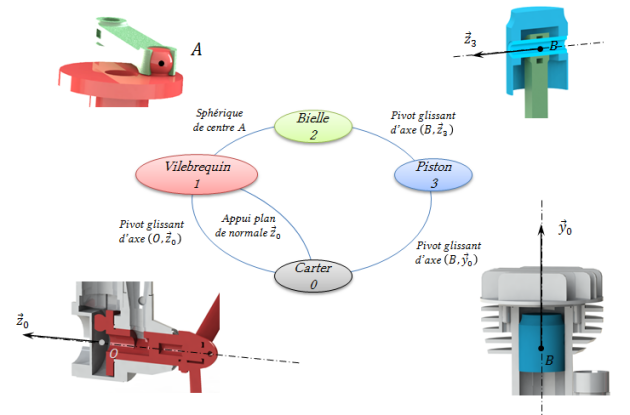
Le graphe des liaisons d'un mécanisme est un modèle qui traduit les liaisons entre les solides et (ou) les classes d'équivalence qui le constituent. Dans ce graphe :
chaque solide ou classe d'équivalence se représente par une bulle contenant le nom ou le numéro de la CEC ;
chaque liaison (ou contact dans un premier temps) se représente par une ligne (ou arc) qui joint deux bulles. Un fois les arcs représentés, on indique la désignation normalisée complète de ces liaisons avec leurs caractéristiques géométriques : centre, axe, normale, directions, etc.
Le graphe de liaisons est donc un outil descriptif qui permet de faire le bilan des associations de solides et des liaisons qui composent un mécanisme.
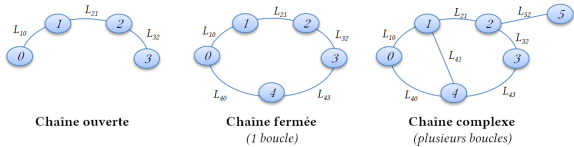
On distingue trois types de chaînes cinématiques de solides reconnaissables à leur graphe des liaisons :
Remarque :
Un arc ne peut relier que deux bulles puisque par définition, une liaison met en jeu 2 solides ou classes d'équivalence.
Un même mécanisme peut avoir un graphe des liaisons différent pour chaque phase de fonctionnement. C'est pourquoi, avant de modéliser un mécanisme, il faut toujours préciser (ou prendre connaissance) de la phase de fonctionnement considérée.
Attention : Erreur grave
Une liaison entre deux classes d'équivalence se détermine en faisant abstraction des autres classes d'équivalence sans tenir compte du reste du mécanisme. Autrement dit, la liaison ne modélise que les mobilités autorisées par les contacts entre les 2 classes d'équivalence concernées donc sans tenir compte du reste du mécanisme.
Exemple : Graphe des liaisons de la phase de fonctionnement normal du micromoteur de modélisme