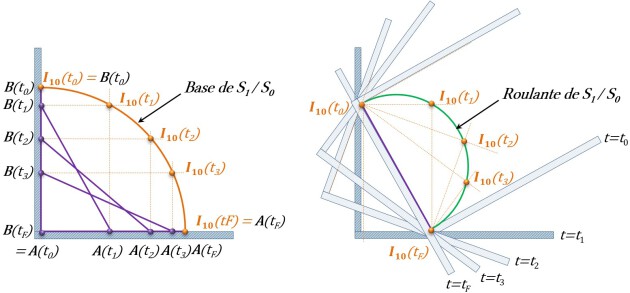
Base et roulante
Soient deux solides \(S_1\) et \(S_0\) en mouvement plan sur plan. On considère que \(S_1\) est en mouvement par rapport à \(S_0\), donc le solide \(S_0\) est pris comme référence.
Définition : Base de S1/S0
La base de \(S_1\) par rapport à \(S_0\) est la trajectoire du CIR de \(S_1/S_0\), \(I_{10}\) dans un plan lié à \(S_0\).
Définition : Roulante de S1/S0
La roulante de \(S_1\) par rapport à \(S_0\) est la trajectoire du CIR de \(S_1/S_0\), \(I_{10}\) dans un plan lié à \(S_1\).
Exemple : Echelle glissant au sol et contre un mur
Une échelle \(S_1\) glisse le long du mur et du sol \(S_0\) sur lequel elle est appuyée. On suppose que le contact n'est jamais rompu aux points d'appui \(A\) et \(B\).
Les vitesses de glissement \(\overrightarrow{V_{A\in S_1/S_0}}\) et \(\overrightarrow{V_{B\in S_1/S_0}}\) sont portées respectivement par \(\vec x_0\) et \(\vec y_0\). La position du CIR\(I_{10}\) se détermine en utilisant les perpendiculaires aux vitesses de glissement passant par A et B.
Fondamental : Propriété
Par définition du CIR, \(\overrightarrow{V_{I_{10}\in S_1/S_0}}=\vec0\). Cela correspond également à la condition de roulement sans glissement d'un solide \(S_1/S_0\) au point \(I_{10}\).
On peut donc conclure qu'à tout instant, la base et la roulante roulent sans glisser l'une sur l'autre au point \(I_{10}\). Les courbes sont donc tangentes en \(I_{10}\) lors du dessin.
Exemple : Echelle glissant au sol et contre un mur
Remarque :
En prenant \(S_1\) comme référence (et plus \(S_0\)), les lieux géométriques de \(I_{10}\) restent les mêmes mais bases et roulantes sont inversées.