Champ des vecteurs vitesse
Mouvement de translation
Rappel : Mouvement de translation
Le champ des vitesses d'un solide \(S_1\) en mouvement de translation par rapport à un solide \(S_0\) est uniforme.
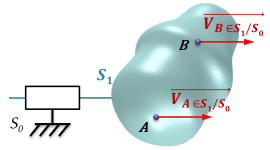
Méthode : Application graphique
Connaissant :
le vecteur vitesse en un point \(A\) de \(S_1\) en mouvement de translation par rapport à \(S_0\),
on peut construire graphiquement le vecteur vitesse de tout point M de \(S_1 /S_0\) :
\(\boxed{ \quad\forall M \in S_1 \, :\,\overrightarrow{V_{M\in S_1/S_0}} = \overrightarrow{V_{A\in S_1/S_0}}\quad}\)
Mouvement de rotation
Rappel : Mouvement de rotation
Soit un solide \(S_1\) en mouvement de rotation d'axe\((A,\vec z_0)\) par rapport à à \(S_0\), à une vitesse angulaire \(\omega_{1/0}\) :
\(\overrightarrow{V_{A\in S_1/S_0}}= \, \vec 0\) ;
les vecteurs vitesse des points liés à \(S_1\) / \(S_0\) sont tangents à la trajectoire et donc dans ce cas perpendiculaires aux « rayons » et à l'axe de rotation \((A, \vec z_0)\) ;
la norme d'un vecteur vitesse est proportionnelle à la distance à l'axe (=rayon \(R\)) et à la vitesse angulaire :
Méthode : Champ des vecteurs vitesse
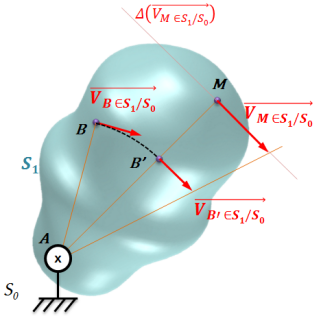
Connaissant :
le vecteur vitesse en un point \(B\) de \(S_1\) dans en mouvement de rotation de centre \(A\) par rapport à \(S_0\) : \(\overrightarrow{V_{B\in S_1/S_0}}\),
on peut construire graphiquement le vecteur vitesse d'un point \(M\) quelconque de \(S_1\) / \(S_0\) :
On trace la droite \((AM)\).
On construit sur la droite (AM) un point B' situé au même rayon que le point \(B\).
On trace \(\overrightarrow{V_{B' \in S_1/S_0}}\), perpendiculaire à \((AM)\) et de même norme que \(\overrightarrow{V_{B\in S_1/S_0}}\) car situé au même rayon.
On trace le support (point d'application + direction) de \(\overrightarrow{V_{M\in S_1/S_0}}\) noté \(\Delta \left(\overrightarrow{V_{M\in S_1/S_0}}\right)\).
On trace le triangle des vitesses traduisant la répartition linéaire des vitesses pour un mouvement de rotation : \(\Vert \, \overrightarrow{V_{M\in S_1/S_0}} \,\Vert = R \times | \omega_{1/0} |\)
On en déduit \(\overrightarrow{V_{M\in S_1/S_0}}\)