Composition des vecteurs vitesse - Application graphique
Rappel
Soit un solide \(S_2\) auquel on associe le repère \(\mathcal{R}_2(O,\vec x_2, \vec y_2, \vec z_2)\) en mouvement par rapport à deux solides \(S_0\) et \(S_1\) auxquels on associe respectivement les repères \(\mathcal{R}_0(O,\vec x_0, \vec y_0, \vec z_0)\) et \(\mathcal{R}_1(O,\vec x_1, \vec y_1, \vec z_1)\).
Pour tout point M appartenant au solide \(S_2\), on a :
Application graphique
Méthode : Composition des vecteurs vitesse
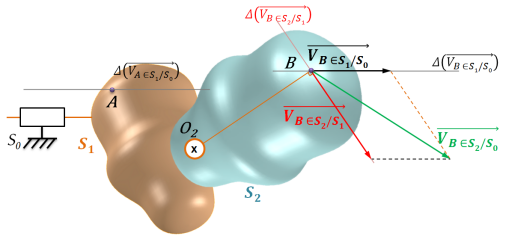
Soient 3 solides \(S_2\), \(S_1\) et \(S_0\) en mouvements relatifs.
Connaissant :
un vecteur vitesse : \(\overrightarrow{V_{B\in S_2/S_0}}\) ,
deux supports en un même point : \(\Delta\overrightarrow{V_{B\in S_2/S_1}}\) et \(\Delta\overrightarrow{V_{B\in S_1/S_0}}\),
on peut construire graphiquement \(\overrightarrow{V_{B\in S_2/S_1}}\) et \(\overrightarrow{V_{B\in S_1/S_0}}\) :
Tracer le vecteur vitesse connu.
Tracer les droites parallèles aux supports connus à chaque extrémités du vecteur vitesse (deux constructions possibles, donnant le même résultat) afin d'obtenir les normes des deux vecteurs vitesse recherchés.
Le sens de ces vecteurs se détermine grâce à la relation de composition des vecteurs vitesse : \(\overrightarrow{V_{B\in S_2/S_0}}\)=\(\overrightarrow{V_{B\in S_2/S_1}}\)+\(\overrightarrow{V_{B\in S_1/S_0}}\).
Cas particulier : composition des vitesses en un point d'un axe de rotation
Fondamental :
Soient deux solides \(S_2\) et \(S_1\) en mouvement sur plan par rapport à un solide \(S_0\) auquel on associe le repère de référence \(\mathcal{R}_0(O_0, \vec x_0, \vec y_0, \vec z_0)\). On suppose que \(S_2\) et \(S_1\) sont en liaison pivot d'axe \((P,\vec z_0)\).
Appliquons la relation de composition des vecteurs vitesse au point \(P\) :
\(\overrightarrow{V_{P\in S_2/S_0}}=\overrightarrow{V_{P\in S_2/S_1}}+\overrightarrow{V_{P\in S_1/S_0}}\).
Or P est sur l'axe de rotation de \(S_2/S_1\), donc par définition d'un mouvement de rotation : \(\overrightarrow{V_{P\in S_2/S_1}}=\vec 0\)
Ainsi : \(\boxed{\quad \overrightarrow{V_{P\in S_2/S_0}}=\overrightarrow{V_{P\in S_1/S_0}} \quad}\)