Système du second ordre

FondamentalFonction de transfert d'un système du second ordre

Un système physique d'entrée e(t) et de sortie s(t) est du 2ème ordre, s'il est régi par une équation différentielle du second ordre à coefficients constants du type :

\(s(t) \, + \, \frac{2.\xi}{\omega_0}\frac {ds(t)}{dt} + \,\, \frac{1}{\omega_0^2}\frac {d^2s(t)}{dt^2}= \,K.e(t)\)

\(\text{ avec : } \left \{\begin{array}{l} \omega_0\text{ : pulsation propre du système non amorti} \textit{ (en rad/s)}\\ \xi\text{ : coefficient d'amortissement (}\xi>0 \textit{ et sans unité)}\\ K \text{ : gain statique}\left( \textit{unité de K = } \frac { \textit{unité } [s]} {\textit{unité }[e]} \right) \\ \end{array} \right .\)

Si les conditions initiales sont nulles (\(s(0)=0\) et \(s'(0)=0\)), la fonction de transfert sous forme canonique s'écrit: \(\boxed{\,\,H(p) = \frac{S(p)}{E(p)}=\frac K {1+\frac{2\xi}{\omega_0}.p+\frac{p^2}{\omega_0^2}}\,\,}\)

Le discriminant du dénominateur vaut : \(\Delta = \frac 4 {\omega_0^2} \left(\xi^2-1\right)\)

Donc les pôles de la fonction de transfert (=racines du dénominateur) dépendent de la valeur du coefficient d'amortissement \(\xi\). Trois cas sont à envisager :

Valeur de \(\xi\)

Expression des pôles

\(\xi>1\)

Régime apériodique

(système amorti)

2 pôles réels :

\(p =- \xi.\omega_0 \pm \omega_0 \sqrt{\xi^2-1}\)

\(\xi=1\)

Régime apériodique critique

(amortissement critique)

1 pôle double :

\(p =- \xi.\omega_0=-\omega_0\)

\(\xi<1\)

Régime pseudo-périodique

(système sous-amorti ou oscillant)

2 pôles complexes conjugués (à partie réelle négative)

\(p =- \xi.\omega_0 \pm j.\omega_0 \sqrt{1-\xi^2}\) , avec \(j^2=-1\)

Réponse indicielle

L'entrée est définie par un échelon d'amplitude \(E_0\) : \(E(p) = \frac{E_0}p\)

La sortie a donc pour expression dans le domaine de Laplace :

\(S(p)=\frac K {1+\frac{2\xi}{\omega_0}.p+\frac{p^2}{\omega_0^2}}.\frac{E_0}p=\frac{K.E_0.\omega_0^2}{(p^2+2.\xi.\omega_0.p+\omega_0^2).p}\)

Pour déterminer la réponse temporelle \(s(t)\) il faut décomposer la fraction rationnelle ci-dessus en éléments simples. Or cette décomposition diffère selon la nature des pôles de la fonction de transfert.

On distingue donc 3 régimes de fonctionnement correspondant à des pôles réels, complexes ou à un pôle double. Toutefois, certaines caractéristiques sont communes à ces 3 régimes de fonctionnement. Elles sont données ci-après.

Caractéristiques communes à tous les régimes de fonctionnement

FondamentalCaractéristiques communes à tous les régimes

  • Valeur finale : ordonnée en \(+\infty\) :

\[s(+\infty)= \underbrace{\lim\limits_{t\rightarrow +\infty } \, s(t) =\lim\limits_{p\rightarrow 0^+ } \,p.S(p)}_{\text{Théorème de la valeur finale}}=\lim\limits_{p\rightarrow 0^+ } \,p.\frac{K.E_0.\omega_0^2}{(p^2+2.\xi.\omega_0.p+\omega_0^2).p}=K.E_0\]

  • Tangente à l'origine :

\[s'(0^+)= \underbrace{\lim\limits_{t\rightarrow 0^+ } \, s'(t) =\lim\limits_{p\rightarrow +\infty } \,p.\left[p.S(p)\right]}_{\text{Théorème de la valeur initiale}}=\lim\limits_{p\rightarrow +\infty } \,p^2.\frac{K.E_0.\omega_0^2}{(p^2+2.\xi.\omega_0.p+\omega_0^2).p}=0\]

  • Erreur statique:

\[ \varepsilon_S= \varepsilon(+\infty)= \lim\limits_{t\rightarrow +\infty } \left[ \, e(t)-s(t) \, \right] =\lim\limits_{p\rightarrow 0^+ } p.\left[ \, \frac {E_0} p - \frac K {1+\frac{2\xi}{\omega_0}.p+\frac{p^2}{\omega_0^2}}.\frac{E_0}p \, \right] =E_0.(1-K)\]
Remarque

  1. Le régime permanent ne dépend que du gain \(K\) et de l'amplitude de l'échelon d'entrée \(E_0\). Il ne dépend ni du coefficient d'amortissement ni de la pulsation propre.

  2. La tangente à l'origine est horizontale, ce qui diffère de la réponse indicielle des systèmes du premier ordre.

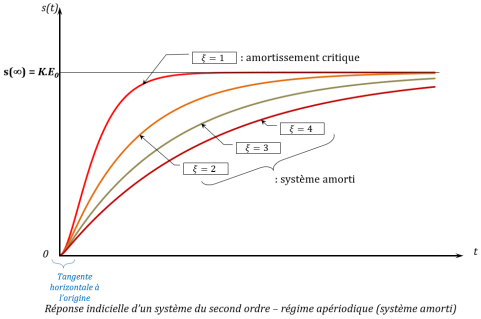
Régime apériodique (système amorti) : ξ>1

Si \(\xi>1\), la fonction de transfert possède deux pôles réels \(p_1\) et \(p_2\) tels que : \(\left \{\begin{array}{l} p_1 = \omega_0 \left(- \xi -\sqrt{\xi^2-1}\right) \\ p_2 = \omega_0 \left(- \xi +\sqrt{\xi^2-1}\right)\\\end{array}\right.\)

La décomposition en éléments simples s'écrit alors :

\(S(p) = \frac{K.E_0.\omega_0^2}{p.(p-p_1)(p-p_2)}=\frac A p +\frac B{(p-p_1)} + \frac C{(p-p_2) }\) avec \(\left \{\begin{array}{l} A=\frac{K.E_0.\omega_0^2}{p_1.p_2}=K.E_0 \quad \text{ car }\quad p_1.p_2={\omega_0^2}\\ \\B=\frac{K.E_0.\omega_0^2}{p_1.(p_1-p_2)}\\ \\C=\frac{K.E_0.\omega_0^2}{p_2.(p_2-p_1)} \end{array}\right.\)

Ainsi, \(S(p) = K.E_0.\left(\frac{1} p +\frac{\omega_0^2}{p_1.(p_1-p_2)}\frac 1{(p-p_1)} +\frac{\omega_0^2}{p_2.(p_2-p_1)} \frac 1{(p-p_2) }\right)\)

En utilisant la transformée de Laplace inverse, on trouve :

\(s(t)=K.E_0.\left( 1+\frac{\omega_0^2}{p_1.(p_1-p_2)} \text e^{p_1.t}+ \frac{\omega_0^2}{p_2.(p_2-p_1)}\text e^{p_2.t}\right).u(t)\)

Enfin, posant \(\tau_1=-\frac 1 {p_1}\) et \(\tau_2=-\frac 1 {p_2}\), et en en utilisant le fait que \(\tau_1.\tau_2=\frac 1 {\omega_0^2}\), on trouve :

\[\boxed{\quad s(t)=K.E_0.\left[1-\frac 1 {\tau_1-\tau_2}.\left( \tau_1. \text e^{-\frac t {\tau_1}}-\tau_2. \text e^{-\frac t {\tau_2}}\right) \right].u(t)\quad }\]
ComplémentNotion de pôle dominant

Dans le cas \(\xi>1\), la fonction de transfert admet donc deux racines réelles et peut également s'écrire, en utilisant la forme suivante :

\[H(p)=\frac K {(1+\tau_1.p)(1+\tau_2.p)}\quad \text{ , avec : } \tau_1=-\frac 1 {p_1} \text{ et }\tau_2=-\frac 1 {p_2}\]

Dans le cas où \(\tau_1 \ll \tau_2\), il est possible de négliger le terme \((1+\tau_1.p)\) devant \((1+\tau_2.p)\) et d'approcher la fonction de transfert par celle d'un premier ordre.

\[H(p) \approx \frac K {1+\tau_2.p}\]

Le pôle \(p_2\) correspond dans ce cas au pôle dominant de la FTBF (celui correspondant à la plus grande constante de temps).

Régime apériodique critique (amortissement critique) : ξ=1

La fonction de transfert admet dans ce cas un pôle double : \(p_1=-\omega_0\)

La décomposition en éléments simples s'écrit alors :

\(S(p) = \frac{K.E_0.\omega_0^2}{p.(p+\omega_0)^2}=\frac A p +\frac B{(p+\omega_0)} + \frac C{(p+\omega_0)^2 }\) avec \(\left \{\begin{array}{l} A=K.E_0 \\B=-A=-K.E_0\\C=-K.E_0.\omega_0 \end{array}\right.\)

La transformée de Laplace inverse donne : \(\boxed{s(t)=K.E_0.\left[1-\text e^{-\omega_0.t}-\omega_0.t.\text e^{-\omega_0.t}\right]}\)

La forme de cette réponse est proche de la précédente mais sa rapidité (\(t_{5\%}\)) est meilleure. Le régime apériodique critique donne la réponse la plus rapide sans dépassement de la valeur finale.

Régime pseudo-périodique (système sous-amorti) : ξ<1

Si \(\xi<1\), la fonction de transfert possède deux pôles complexes conjugués \(p_1\) et \(p_2\) tels que : \(\left \{\begin{array}{l} p_1 = \omega_0 \left(- \xi -j \sqrt{1-\xi^2}\right) \\ p_2 = \omega_0 \left(- \xi +j \sqrt{1-\xi^2}\right)\\\end{array}\right.\)

La sortie dans le domaine de Laplace s'écrit : \(S(p)=\frac {K.E_0} {\left(1+\frac{2\xi}{\omega_0}.p+\frac{p^2}{\omega_0^2}\right).p}\)

On peut alors utiliser directement le "tableau" des transformées de Laplace pour déterminer la transformée inverse et obtenir l'expression de la sortie dans le domaine temporel s(t) :

\(\boxed{s(t)=K.E_0.\left( 1-\frac{\text e^{-\xi.\omega_0.t}}{\sqrt{1-\xi^2}} .\sin (\omega_0.\sqrt{1-\xi^2}.t+\varphi)\right)} \quad \text{ avec : }\cos \varphi = \xi\)

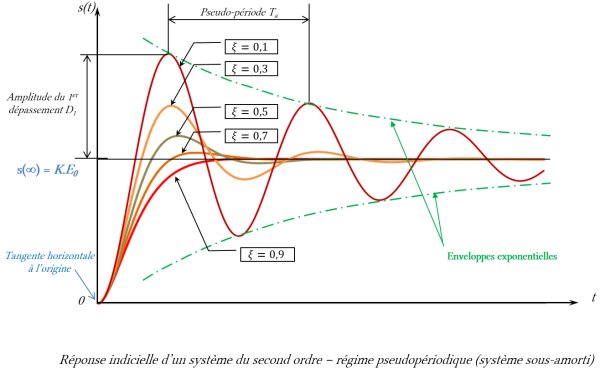
FondamentalPseudo-période :

La réponse présente des oscillations amorties dont la période, appelée pseudo-période, est :

\[\boxed{T_a=\frac{2\pi}{\omega_0\sqrt{1-\xi^2}}=\frac{2\pi}{\omega_a}} \quad , \omega_a=\omega_0.\sqrt{1-\xi^2} \text{ : pulsation propre du système amorti}\]
FondamentalDépassements absolus et relatifs :

  • Instant du k-ième dépassement :

\[\boxed{t_k=k.\frac {T_a} 2 = \frac{k. \pi} {\omega_0\sqrt{1-\xi^2}}} \;, k\in \mathbb N^*\]

  • Amplitude du k-ième dépassements (absolus) :

\[ \boxed{D_{r,k}=\left| s(\infty)-s(t_k)\right|=K.E_0.\text e ^{-k\frac {\xi.\pi}{\sqrt{1-\xi^2}}}} \;, k\in \mathbb N^* \]

  • Amplitude du k-ième dépassements relatif :

\[ \boxed{D_{r,k}= \frac{D_k} {s(\infty)}=\left| \frac{s(\infty)-s(t_k)}{s(\infty)}\right|=\text e ^{-k\frac {\xi.\pi}{\sqrt{1-\xi^2}}}} \;, k\in \mathbb N^* \]

On peut remarquer que les dépassements relatifs ne dépendent que du coefficient d'amortissement.

ConseilA savoir redémontrer rapidement ou à apprendre :
\[\forall \xi\in ]0,1[, \, \forall k\in \mathbb N^*\quad D_{r,k}=\text e ^{-k\frac {\xi.\pi}{\sqrt{1-\xi^2}}} \quad \Leftrightarrow \quad \boxed{\xi=\sqrt{\frac {(\ln D_{r,k})^2}{(k.\pi)^2+(\ln D_{r,k})^2}}}\]

  • Temps de réponse à 5% \(t_{5\%}\) :

Il n'existe pas de formule simple pour calculer le temps de réponse à 5% car il dépend de la valeur du coefficient d'amortissement \(\xi\) et de la pulsation propre non amortie du système \(\omega_0\).

On utilise plutôt l'abaque donné ci-dessous qui donne la valeur du temps de réponse réduit \(t.\omega_0\) en fonction du coefficient d'amortissement \(\xi\).

FondamentalTemps de réponse

  • Le temps de réponse à 5% minimum est obtenue pour \(\boxed{ \, \xi=0,7 \,} \) :

\[ \xi=0,7, \quad \Rightarrow \quad t_{5\%}.\omega_0\approx 3 \quad \Rightarrow \quad \boxed{t_{5\%}=\frac 3 {\omega_0}}\]

  • Le temps de réponse à 5% minimum sans dépassement est obtenue pour \(\boxed{ \, \xi=1 \,}\) :

\[ \xi=1, \quad \Rightarrow \quad t_{5\%}.\omega_0\approx 5 \quad \Rightarrow \quad \boxed{t_{5\%}=\frac 5 {\omega_0}}\]