Système du premier ordre

FondamentalFonction de transfert d'un système du premier ordre

Un système physique d'entrée \(e(t)\) et de sortie \(s(t)\) est du 1er ordre, s'il est régi par une équation différentielle du 1er ordre à coefficients constants du type : \(\tau \frac{ds(t)}{dt} +s(t) = K.e(t)\)

avec \(\left \{\begin{array}{l} \tau \text{ : constante de temps du système } (\textit{en seconde }) \\ K \text{ : gain statique } \left( \textit{unité de K = } \frac { \textit{unité } [s]} {\textit{unité }[e]} \right) \\ \end{array} \right .\)

Si les conditions initiales sont nulles (\(s(0)=0\)), la fonction de transfert sous forme canonique s'écrit : \(\boxed{\,\,H(p) = \frac{S(p)}{E(p)}=\frac K {1+\tau.p}\,\,}\)

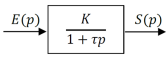
Réponse indicielle

L'entrée est définie par un échelon d'amplitude \(E_0\) : \(E(p) = \frac{E_0}p\)

La sortie a donc pour expression dans le domaine de Laplace :

\(S(p)=\frac K {1+\tau.p}. \frac{E_0}p =\underbrace{\frac {K.E_0}p-\frac{K.\tau.E_0}{1+\tau.p}}_{\textit{Décomposition en éléments simples}}\)

La réponse temporelle s'écrit alors : \(\boxed{ \,\, s(t)=K.E_0.\left(1-\text{e}^{-\frac t \tau}\right) .u(t)\, \, }\)

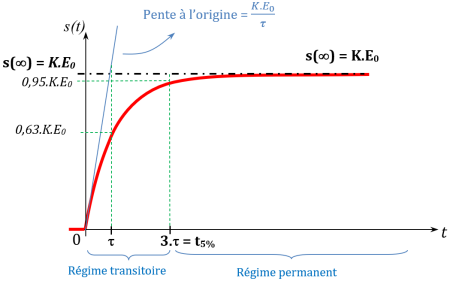
  • Valeur finale : ordonnée en \(+\infty\) :

\[s(+\infty)= \underbrace{\lim\limits_{t\rightarrow +\infty } \, s(t) =\lim\limits_{p\rightarrow 0^+ } \,p.S(p)}_{\text{Théorème de la valeur finale}}=\lim\limits_{p\rightarrow 0^+ } \,p.\frac K {1+\tau.p}. \frac{E_0}p=K.E_0\]

  • Pente à l'origine :

\[s'(0^+)= \underbrace{\lim\limits_{t\rightarrow 0^+ } \, s'(t) =\lim\limits_{p\rightarrow +\infty } \,p.\overbrace{\left[p.S(p)\right]}^{\text{Transformée de la dérivée}}}_{\text{Théorème de la valeur initiale}}=\lim\limits_{p\rightarrow +\infty } \,p^2.\frac K {1+\tau.p}. \frac{E_0}p=\frac{K.E_0}\tau\]

  • Temps de réponse à 5%, \(t_{5\%}\):

On cherche \(t_{5\%}\) tel que :

\[s(t_{5\%} )=0,95.s(+\infty)=0,95.K.E_0\]

Soit :

\[\begin{eqnarray*} &K.E_0.\left( 1-\text e^{-\frac{t_{5\%}}\tau} \right)=0,95.K.E_0 \Rightarrow e^{-\frac{t_{5\%}}\tau} =0,05\\ &\Rightarrow\boxed{t_{5\%}=-\ln(0,05).\tau\approx 3\tau} \end{eqnarray*} \]

  • Réponse à \(t=\tau\):

\[s(\tau)=K.E_0.\left(1-\text e^{-1}\right)=0,63.K.E_0\]

  • Erreur statique:

\[ \varepsilon_S= \varepsilon(+\infty)= \lim\limits_{t\rightarrow +\infty } \left[ \, e(t)-s(t) \, \right] =\lim\limits_{p\rightarrow 0^+ } p.\left[ \, \frac {E_0} p - \frac K {1+\tau.p}.\frac{E_0}p \, \right] =E_0.(1-K)\]

Réponse impulsionnelle

L'entrée est définie par une impulsion de Dirac : \(e(t)= \delta(t) \quad \xrightarrow[]{\mathcal{L}^{}} \quad E(p) = 1\)

La sortie a donc pour expression dans le domaine de Laplace : \(S(p)=\frac K {1+\tau.p}. 1=\frac {\frac K \tau}{\frac 1 \tau+p}\)

La réponse temporelle s'écrit : \(\boxed{ \,\, s(t)=\frac K \tau \,\text{e}^{-\frac t \tau} .u(t)\, \, }\)

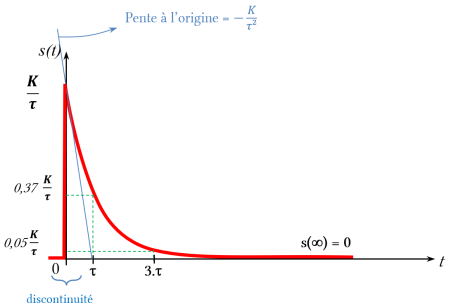
Réponse à une rampe

L'entrée est définie par une rampe : \(e(t)= a.t.u(t) \quad \xrightarrow[]{\mathcal{L}^{}} \quad E(p) = \frac a {p^2}\)

La sortie a donc pour expression dans le domaine de Laplace :

\(S(p)=\frac K {1+\tau.p}. \frac a {p^2}=\underbrace{\frac {K.a.\tau^2} {1+\tau.p}-\frac {K.a.\tau} {p}+\frac {K.a} {p^2}}_{\textit{Décomposition en éléments simples}}\)

La réponse temporelle s'écrit : \(\boxed{ \,\, s(t)=K .a .\left( t-\tau+\tau.\text{e}^{-\frac t \tau}\right).u(t) }\)

  • Valeur finale : ordonnée en \(+\infty\) :

\[s(+\infty)= \underbrace{\lim\limits_{t\rightarrow +\infty } \, s(t) =\lim\limits_{p\rightarrow 0^+ } \,p.S(p)}_{\text{Théorème de la valeur finale}}=\lim\limits_{p\rightarrow 0^+ } \,p.\frac K {1+\tau.p}. \frac a {p^2}=+\infty \quad (K>0)\]

  • Pente à l'origine :

\[s'(0^+)= \underbrace{\lim\limits_{t\rightarrow 0^+ } \, s'(t) =\lim\limits_{p\rightarrow +\infty } \,p.\overbrace{\left[p.S(p)\right]}^{\text{Transformée de la dérivée}}}_{\text{Théorème de la valeur initiale}}=\lim\limits_{p\rightarrow +\infty } \,p^2.\frac K {1+\tau.p}. \frac a {p^2}=0\]

  • Etude asymptotique en \(+\infty\):

Lorsque \(t \rightarrow +\infty\), le terme \(\tau.\text e^{-\frac t \tau}\rightarrow 0\). Par conséquent,\(s(t) \rightarrow a.K.(t-\tau)\). L'asymptote a donc pour équation \(y(t)=a.K.(t-\tau)\). Elle coupe l'axe des abscisses à \(t=\tau\) et a pour pente : \(a.K\)

  • Erreur de trainage:

\[ \varepsilon_v= \varepsilon(+\infty)= \lim\limits_{t\rightarrow +\infty } \left[ \, e(t)-s(t) \, \right] =\underbrace{\lim\limits_{t\rightarrow +\infty } \left[ \, a.t.(1-K).u(t) \right]}_{\text{dépend de la valeur de K}}+K .a .\tau \]