Système intégrateur
Fondamental :
L'équation liant l'entrée et la sortie est : \(\frac{ds(t)}{dt} = K.e(t)\)
La fonction de transfert s'écrit (conditions initiales nulles) :
\(\boxed{\,\,H(p) = \frac{S(p)}{E(p)}=\frac K p\,\,}\)
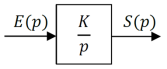
Réponse à un échelon d'amplitude\(E_0\)
\(\begin{eqnarray*} e(t)= E_0. u(t) \quad & \xrightarrow[]{\mathcal{L}^{}} & \quad E(p) = \frac{E_0}p \\ S(p) = \frac K p.E(p)=\frac{K.E_0}{p^2}\quad & \xrightarrow[]{\mathcal{L}^{-1}} & \quad s(t)=K.E_0.t.u(t)\end{eqnarray*}\)
