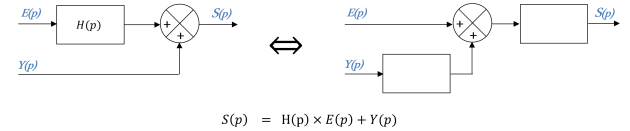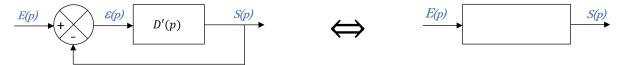Recherche de la fonction de transfert par manipulation des schéma-blocs
Représentation par schéma-blocs et fonctions de transfert
Afin de prévoir les performances simulées d'un système, il est nécessaire de déterminer sa fonction de transfert. Comme nous venons de le voir, cela peut se faire directement à partir de la manipulation des équations dans le domaine symbolique de Laplace. Cependant, dans le cas des systèmes plus complexes, cela peut conduire à manipuler un grand nombre d'équations entraînant souvent des erreurs de calculs.
On privilégie dans ce cas une méthode davantage graphique consistant tout d'abord à représenter le système sous forme de schéma-blocs : chacun de ses composants est modélisé par un bloc contenant sa fonction de transfert ; l'association des blocs élémentaires conduit au schéma-blocs complet du système [voir annexe 4].
Enfin, la manipulation de ce schéma-blocs selon des règles décrites ci-après permet de calculer la fonction de transfert globale du système.
Blocs en série
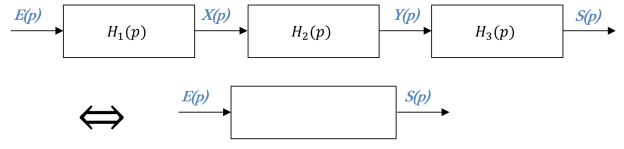
Dans le cas de blocs en série, on a :
\(\left \{\begin{array}{l}S(p)=H_3(p)\times Y(p) \\ Y(p)=H_2(p)\times X(p)\\X(p) = H_1(p)\times E(p)\\ \end{array}\right . \Rightarrow \quad S(p)=H_3(p)\times H_2(p)\times H_1(p)\times E(p)\)
Blocs en parallèle
On a : \(S(p) = H_1(p).E(p) + H_2 (p).E(p) = \left(H_1 (p)+ H_2 (p)\right).E(p)\)
On peut donc remplacer ces deux blocs et le sommateur par un seul bloc dont la fonction de transfert est la somme de \(H_1(p)\) et \(H_2(p)\).
Déplacement d'un point de prélèvement
Déplacement vers la droite :
Lors du déplacement vers la droite d'un point de prélèvement (par-dessus un bloc \(H(p)\)), il faut rajouter après le point un bloc de fonction de transfert \(\frac 1{H(p)}\).
Déplacement vers la gauche :
Comme : \(S(p) = H(p)E(p)\) , lors du déplacement vers la gauche d'un point de prélèvement (par-dessus un bloc\(H(p)\)), il faut rajouter après le prélèvement un bloc de fonction de transfert \(H(p)\).
Déplacement d'un sommateur/soustracteur
Déplacement vers la droite :
Déplacement vers la gauche :
Fonction de transfert en boucle fermée (FTBF) et en boucle ouverte (FTBO)
Les systèmes asservis sont par définition bouclés. Le modèle de base d'une boucle est le suivant :
Fonction de transfert de la chaîne directe : D(p)
Fonction de transfert de la boucle de retour : R(p)
Fonction de Transfert en Boucle Ouverte (FTBO) :
Pour calculer la FTBO, on ouvre le schéma-blocs au niveau du comparateur.
La FTBO est égale au produit des fonctions de transfert de chaque bloc de la boucle ouverte : \(\boxed{FTBO(p) = \frac{Y(p)}{E(p)} = D(p)\times R(p)}\)
La FTBO est utilisée pour déterminer les conditions de stabilité et de précision d'un système asservi.
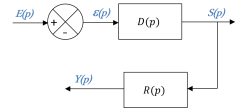
Fonction de Transfert en Boucle Fermée (FTBF)
La fonction de transfert équivalente de la boucle : \(\boxed{FTBF(p)=\frac{S(p)}{E(p)}=\frac{D(p)}{1+R(p)\times D(p)}}\)
Preuve :
Cas particulier du retour unitaire :
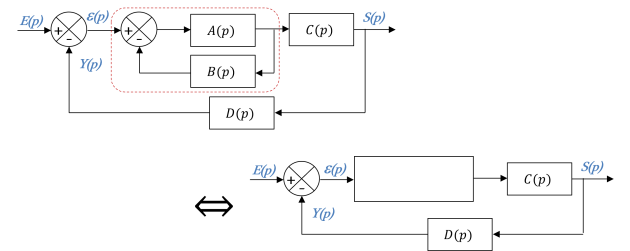
Systèmes à boucles concentriques
Pour ce type de système, il faut toujours commencer par calculer la FTBF de la boucle interne.
On reconnaît ensuite une boucle fermée que l'on sait bien traiter.
Systèmes à boucles imbriquées
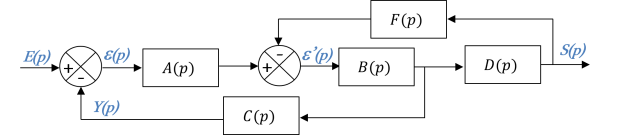
Pour ce type de système, il faut toujours commencer par déplacer les points de prélèvement pour se ramener à un système de boucles concentriques.
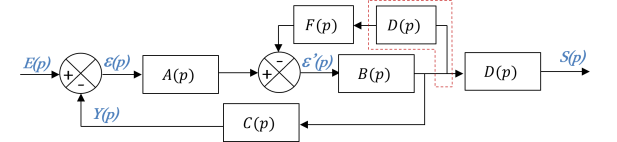
On se retrouve ensuite devant un système à boucles concentriques que l'on sait aussi bien traiter.
FTBF des systèmes à deux entrées : principe de superposition
De manière générale, dans un système réel, plusieurs entrées aboutissent à une sortie. Ces entrées comprennent non seulement l'entrée principale (grandeur par rapport à laquelle on détermine la sortie) mais aussi des entrées supplémentaires très souvent parasites (bruit, effort résistant,...) appelées perturbations.
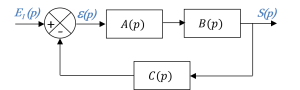
Le schéma bloc générique d'un tel système est le suivant :
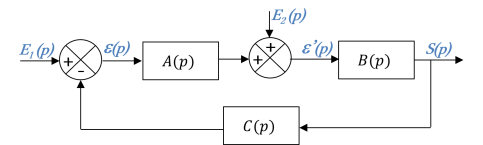
Ce schéma bloc possède deux entrées : \(E_1(p)\) est l'entrée principale et \(E_2(p)\) une entrée secondaire.
Fondamental : Principe de superposition
Pour déterminer la réponse d'un système soumis à deux entrées, on utilise le principe de superposition des SLCI. Le schéma est alors équivalent à la superposition de deux schémas : l'un pour lequel \(E_2(p)=0\), et l'autre en prenant \(E_1(p)=0\). La mise en oeuvre de ce principe s'effectue en 3 étapes :
Calculer la fonction de transfert \(H_1(p)=\left.\frac{S(p)}{E_1(p)}\right|_{E_2(p)=0}\) en supposant\(E_2(p)=0\).
Calculer la fonction de transfert \(H_2(p)=\left.\frac{S(p)}{E_2(p)}\right|_{E_1(p)=0}\) en supposant\(E_1(p)=0\).
Donner l'expression de la sortie S(p) en additionnant (superposant) l'expression des sorties obtenues dans les 2 cas précédents :
Exemple : Application du principe de superposition
En utilisant le schéma bloc générique d'un système à deux entrées :
1. Fonction de transfert \(H_1(p)\) pour \(E_2(p)=0\)
\(H_1(p)=\left.\frac{S(p)}{E_1(p)}\right|_{E_2(p)=0}=\frac{A(p).B(p)}{1+A(p).B(p).C(p)}\)
2. Fonction de transfert \(H_2(p)\) pour \(E_1(p)=0\)
3. Le principe de superposition permet d'obtenir la fonction de transfert en boucle fermée du système:
Remarque :
Les fonctions \(H_1(p)\) et \(H_2(p)\) ont le même dénominateur.