Modélisation par équation différentielle
D'une manière générale, un système linéaire continu invariant peut être modélisé grâce aux lois de la physique par une équation différentielle, linéaire et à coefficients constants reliant la sortie s(t) à l'entrée e(t) de la forme :
Dans un système causal, c'est-à-dire lorsque la cause précède l'effet (tout système physique) : \(n \geq m\). Ainsi le degré de dérivation le plus élevé sur la sortie correspond à l'ordre du système. On parle de système d'ordre n.
Deux modèles de systèmes fondamentaux sont couramment rencontrés et étudiés dans le cadre de la PTSI : les systèmes du premier ordre et les systèmes du second ordre.
Cas d'un système du premier ordre
La forme générale de l'équation différentielle caractéristique d'un système du premier ordre simple est :
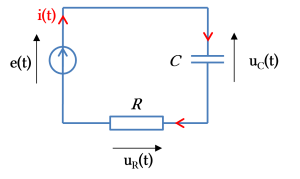
Exemple : Circuit R,C
D'après la loi des mailles, on a : \(e(t ) = u_R(t )+ u_C(t )\)
Connaissant la relation de comportement aux bornes d'un condensateur : \(i (t ) = C\,\frac {d u_C(t)}{d t}\) , et celle d'une résistance : \(u_R (t ) = R . i (t )\), on a donc :
On cherche donc à résoudre l'équation différentielle suivante :
On détermine alors la constante de temps du système : \(\tau=R.C\) et le gain statique : \(K =1\).
Cas d'un système du second ordre
La forme générale de l'équation différentielle caractéristique d'un système du second ordre simple est :
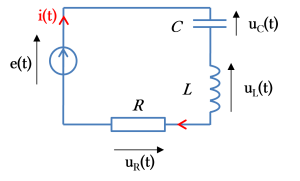
Exemple : Circuit R,L,C
D'après la loi des mailles, on a : \(e(t ) = u_R(t )+u_L(t)+ u_C(t )\)
Connaissant la relation de comportement aux bornes d'une bobine : \(u_L (t ) = L\,\frac {d i(t)}{d t}\) , et celle d'une résistance : \(u_R (t ) = R . i (t )\), on a donc :
En utilisant alors la relation de comportement aux bornes d'un condensateur : \(i (t ) = C\,\frac {d u_C(t)}{d t}\) , on obtient l'équation différentielle suivante :
On détermine alors la pulsation propre du système non amorti \(\omega_0\), le coefficient d'amortissement \(\xi\) et le gain statique \(K\).