Transformée de Laplace inverse

La transformée de Laplace étant bijective (propriété d'unicité), la transformée inverse existe et permet de retrouver le comportement temporel d'un système (évolution de la sortie en fonction du temps), à partir de son étude dans le domaine de Laplace.

\[F(p) \xrightarrow[]{\mathcal{L}^{-1}} f(t)\]

Si l'on connaît la fonction de transfert \(H(p)\) d'un système, ainsi que l'entrée \(E(p)\), alors nous pourrons en déduire la sortie \(S(p)\) dans le domaine de Laplace :

\[S(p)=H(p).E(p) \quad \Rightarrow \quad S(p) = \frac{ b_0+b_1.p+...+b_m.p^m}{a_0+a_1.p+...+a_n.p^n} . E(p) \]

Pour calculer la réponse temporelle \(s(t)\), il faut calculer la transformée inverse de \(S(p)\) en utilisant le tableau des transformée de Laplace usuelles. Or les fonctions de transfert des systèmes étudiés ont souvent des expressions complexes conduisant à des fonctions de sortie également complexes, qu'il faut tout d'abord simplifier. Ainsi, le calcul de la réponse temporelle \(s(t)\) s'effectue généralement en trois temps :

  1. Décomposer en éléments simples la fonction \(S(p)\) [voir annexe 3]. .

  2. Calculer la transformée inverse de chaque élément simple en procédant par identification de ces éléments simples à des fonctions connues.

  3. Effectuer la somme de ces transformées inverses.

Remarque

Le calcul de la transformée de Laplace inverse n'est plus au programme des CPGE. Cependant son utilisation est présentée ici car elle permet de démontrer certains résultats de cours que vous pourrez utiliser directement dans un souci d'efficacité.

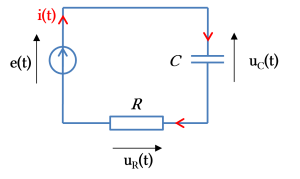
ExempleCircuit RC

On rappelle l'équation différentielle traduisant le comportement du circuit RC pour différents types de signaux en entrée e(t) : \(R.C\frac {d u_C(t)}{d t}+ u_C(t ) = e(t)\)

On souhaite déterminer l'évolution temporelle de la tension aux bornes du condensateur \(u_c(t)\) pour une tension constante \(e(t)=e_0\) imposée aux bornes du générateur

  • Étape 1 : transformation de Laplace de l'équation différentielle

\[R.C\frac {d u_C(t)}{d t}+ u_C(t) = e(t) \quad \xrightarrow[\text{ C.I. nulle : }u_C(0^+)]{\mathcal{L}} \quad R.C.p.U_C(p) + U_C(p)=E(p) \]

  • Étape 2 : calcul de la fonction de transfert

\[R.C.p.U_C(p) + U_C(p)=E(p) \quad \Rightarrow \quad H(p)=\frac{U_C(p)}{E(p)}=\frac 1 {1+R.C.p}\]

  • Étape 3 : expression de la sortie \(S(p)\) pour une entrée en échelon d'amplitude \(e_0\)

\[ e(t)=e_0.u(t) \quad \xrightarrow[]{\mathcal{L}} \quad E(p)=\frac{e_0} p \]
\[\text{Ainsi : } H(p) = \frac{U_C(p)}{E(p)} \quad \Rightarrow \quad U_c(p) = \frac 1 {1+R.C.p}.\frac{e_0} p\]

  • Étape 4 : transformation de Laplace inverse

\[\textbf{Etape 4.a}\text{ : décomposition en éléments simples}\]
\[U_c(p) = \frac 1 {1+R.C.p}.\frac{e_0} p \quad \rightarrow \quad U_c(p) = \frac{e_0} p - \frac {e_0} {p+\frac 1 {R.C}}\]
\[\textbf{Etape 4.b}\text{ : transformation de Laplace inverse des éléments simples}\]
\[\frac{e_0} p \quad \xrightarrow[]{\mathcal{L}^{-1}} \quad e_0.u(t) \quad \text{ et } \quad -\frac {e_0} {p+\frac 1 {R.C}} \quad \xrightarrow[]{\mathcal{L}^{-1}} \quad -{e_0}.\text{e}^{\left(- \frac t {R.C}\right)} .u(t)\]
\[\textbf{Etape 4.c}\text{ : somme des transformées inverses}\]
\[u_c(t)=e_0.u(t) -e_0.\text{e}^{\left(- \frac t {R.C}\right)} .u(t)\]

Au final : \(\boxed{u_c(t)=e_0 .\left( 1-\text{e}^{- \frac t {R.C}} \right).u(t)}\)

Remarque

L'étape 4 n'étant plus au programme des CPGE, il s'agira dans votre cas de reconnaître à l'étape n°2 une fonction de transfert caractéristique d'un système du premier ordre. Une fois la partie suivante de ce cours traitée et maîtrisée (partie 4 : « Réponse temporelle des systèmes fondamentaux»), vous pourrez donner directement l'allure de l'évolution temporelle de la réponse du système à un échelon de tension et déterminer ses performances simulées (stabilité, précision, rapidité,...).