Roulement et pivotement
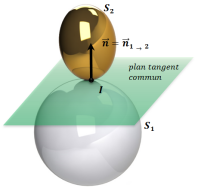
Soient deux solides \(S_1\) et \(S_2\) en contact en un point I. On peut définir :
des surfaces de contact ;
un plan tangent commun aux deux surfaces en contact ;
une normale au contact \(\vec n\).
Définition : Vecteurs taux de rotation de pivotement et de roulement S2/S1
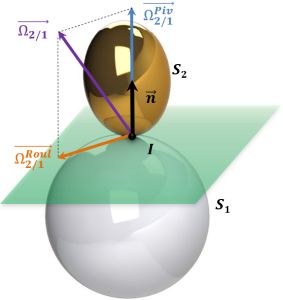
Soit \(\overrightarrow{\Omega_{2/1}}\) le vecteur taux de rotation du solide \(S_2\) par rapport au solide \(S_1\). Posons \(\overrightarrow{\Omega_{2/1}}=\overrightarrow{\Omega^{Piv}_{2/1}}+\overrightarrow{\Omega^{Roul}_{2/1}}\), avec :
\(\overrightarrow{\Omega^{Piv}_{2/1}}\) : vecteur taux de rotation de pivotement de \(S_2/S_1\)
Il s'agit de la composante normale de \(\overrightarrow{\Omega_{2/1}}\).
Elle est donc portée par la normale \(\vec n=\vec n_{1\rightarrow 2}\) :
\(\boxed{ \quad\overrightarrow{\Omega^{Piv}_{2/1}} = \left( \, \overrightarrow{\Omega_{2/1}} \, .\, \vec n \, \right) \, \, \vec n\quad}\)
\(\overrightarrow{\Omega^{Roul}_{2/1}}\) : vecteur taux de rotation de roulement de \(S_2/S_1\)
Il s'agit de la composante tangentielle de \(\overrightarrow{\Omega_{2/1}}\).
Elle est contenue dans le plan tangent commun à \(S_2\) et \(S_1\) :
\(\boxed{\quad\overrightarrow{\Omega^{Roul}_{2/1}} =\overrightarrow{\Omega_{2/1}}- \underbrace{\overrightarrow{\Omega^{Piv}_{2/1}}}_{ \left( \, \overrightarrow{\Omega_{2/1}} \, .\, \vec n \, \right) \, \, \vec n}\quad}\)