Limites de l'étude : linéarité, continuité, invariance
En PTSI, nous nous limiterons à l'étude et à la modélisation des systèmeslinéaires continus et invariants (SLCI).
Linéarité
Un système est dit linéaire si la relation qui décrit son comportement est elle-même linéaire. D'un point de vue mathématique, le comportement d'un système se modélise par des équations différentielles reliant entrées et sorties.
Fondamental : Système linéaire
Un système est dit linéaire si la relation entre la grandeur d'entrée et la grandeur de sortie s'exprime sous forme d'une équation différentielle à coefficients constants du type :
Propriétés
Un système linéaire vérifie le principe de superposition:
Dans le cas d'une loi de comportement non-linéaire, il est possible de linéariser localement le comportement du système au voisinage d'un point de fonctionnement en remplaçant localement le comportement non-linéaire du système par un comportement linéaire approché. Cette linéarisation ne sera pertinente que sur un intervalle précis des entrées, autour du point de fonctionnement. Au delà, un nouveau modèle sera appliqué.
Continuité
Fondamental : Système continu
Un système est continu, par opposition à un système discret, lorsque des variations des grandeurs physiques de sortie qui le caractérisent sont des fonctions du temps continues et que l'on peut donc définir ces grandeurs à chaque instant (\(\forall t \geq 0\)). On parle aussi dans ce cas de système analogique.
La plupart des systèmes physiques, d'un point de vue macroscopique, sont continus. Dans les systèmes de commande modernes, l'information est traitée, le plus souvent, par des systèmes informatiques ce qui nécessite la numérisation des signaux. On parle dans ce cas de systèmes échantillonnés ou discrets.
Lorsqu'un signal continu est numérisé pour être traité par un micro-contrôleur il subit deux discrétisations :
Un échantillonnage en temps : la valeur du signal est prélevée tous les pas de temps (elle est considérée comme constante au cours du pas de temps par le système de commande).
Une quantification : la mesure est mémorisée de façon discrète dans le contrôleur. L'intervalle de mesure est décomposé en N pas de mesure, la valeur retenue étant le pas le plus proche de la valeur mesurée.
Très souvent, la période d'échantillonnage est très inférieure au temps de réponse du système (quelques microsecondes pour l'échantillonnage contre quelques millisecondes pour le processus), si bien qu'il est alors possible d'assimiler le comportement à celui d'un système continu.
Invariance
Fondamental : Système invariant
Un système invariant est un système dont les caractéristiques de comportement ne se modifient pas dans le temps. Autrement dit, le système ne vieillit pas.
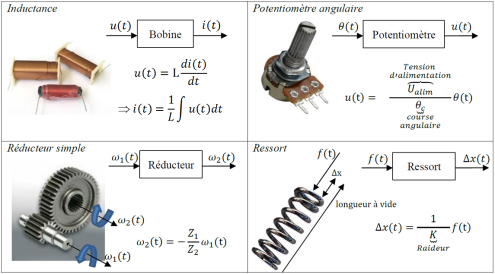
Exemples de composants linéaires continus invariants
Dans la réalité, bien qu'étant souvent continus, les systèmes ne sont pas tout à fait linéaires (voir les lois entrée/sortie établies en TP, phénomènes de saturation, hystérésis, etc.) ni invariants (échauffement, usure, variation de masse,etc.).
Cependant, les modèles retenus pour modéliser leur comportement possèdent ces propriétés et permettent d'obtenir dans bien des cas un bonne approximation du comportement réel. Il faut cependant conserver à l'esprit que ces hypothèses induisent nécessairement un écart entre les performances mesurées et simulées.